The line through A(4, 7) with gradient m meets the x-axis at P and the y-axis at R. The line through B(8, 3) with gradient −1m meets the x-axis at Q and the y-axis at S. Find in term of m, the co-ordinates of P, Q, R and S. Obtain expressions for OP. OQ and OR. OS, where O is the point (0, 0).
The correct Answer is:P(4m−7m,0),Q(3m+8,0),R(0,−4m+7),S(0,3m+8m)OP.OQ=1m(4m−7)(3m+8),andOR.OS=−1m(4m−7)(3m+8)
To solve the problem step by step, we will find the coordinates of points P, Q, R, and S in terms of the gradient m and then derive the expressions for OP, OQ, OR, and OS.
Step 1: Find the coordinates of point P
The line through point A(4, 7) with gradient m can be expressed using the point-slope form of the line equation:
y−7=m(x−4)
To find point P where the line meets the x-axis, we set y=0:
0−7=m(x−4)
This simplifies to:
−7=m(x−4)
Solving for x:
x−4=−7m⟹x=4−7m
Thus, the coordinates of point P are:
P(4−7m,0)
Step 2: Find the coordinates of point R
To find point R where the line meets the y-axis, we set x=0:
y−7=m(0−4)
This simplifies to:
y−7=−4m⟹y=7−4m
Thus, the coordinates of point R are:
R(0,7−4m)
Step 3: Find the coordinates of point Q
The line through point B(8, 3) with gradient −1m can be expressed as:
y−3=−1m(x−8)
To find point Q where the line meets the x-axis, we set y=0:
0−3=−1m(x−8)
This simplifies to:
−3=−1m(x−8)⟹3m=x−8⟹x=3m+8
Thus, the coordinates of point Q are:
Q(3m+8,0)
Step 4: Find the coordinates of point S
To find point S where the line meets the y-axis, we set x=0:
y−3=−1m(0−8)
This simplifies to:
y−3=8m⟹y=3+8m
Thus, the coordinates of point S are:
S(0,3+8m)
Step 5: Obtain expressions for OP, OQ, OR, and OS
Now we will find the distances from the origin O(0, 0) to points P, Q, R, and S.
1. Distance OP:
OP=√(4−7m)2+02=∣∣∣4−7m∣∣∣
2. Distance OQ:
OQ=√(3m+8)2+02=|3m+8|
3. Distance OR:
OR=√02+(7−4m)2=|7−4m|
4. Distance OS:
OS=√02+(3+8m)2=∣∣∣3+8m∣∣∣
Summary of Coordinates:
- P(4−7m,0)
- Q(3m+8,0)
- R(0,7−4m)
- S(0,3+8m)
Summary of Distances:
- OP=∣∣∣4−7m∣∣∣
- OQ=|3m+8|
- OR=|7−4m|
- OS=∣∣∣3+8m∣∣∣
The line through point A(4, 7) with gradient m can be expressed using the point-slope form of the line equation:
y−7=m(x−4)
To find point P where the line meets the x-axis, we set y=0:
0−7=m(x−4)
This simplifies to:
−7=m(x−4)
Solving for x:
x−4=−7m⟹x=4−7m
Thus, the coordinates of point P are:
P(4−7m,0)
To find point R where the line meets the y-axis, we set x=0:
y−7=m(0−4)
This simplifies to:
y−7=−4m⟹y=7−4m
Thus, the coordinates of point R are:
R(0,7−4m)
The line through point B(8, 3) with gradient −1m can be expressed as:
y−3=−1m(x−8)
To find point Q where the line meets the x-axis, we set y=0:
0−3=−1m(x−8)
This simplifies to:
−3=−1m(x−8)⟹3m=x−8⟹x=3m+8
Thus, the coordinates of point Q are:
Q(3m+8,0)
To find point S where the line meets the y-axis, we set x=0:
y−3=−1m(0−8)
This simplifies to:
y−3=8m⟹y=3+8m
Thus, the coordinates of point S are:
S(0,3+8m)
Now we will find the distances from the origin O(0, 0) to points P, Q, R, and S.
OP=√(4−7m)2+02=∣∣∣4−7m∣∣∣
OQ=√(3m+8)2+02=|3m+8|
OR=√02+(7−4m)2=|7−4m|
OS=√02+(3+8m)2=∣∣∣3+8m∣∣∣
- P(4−7m,0)
- Q(3m+8,0)
- R(0,7−4m)
- S(0,3+8m)
- OP=∣∣∣4−7m∣∣∣
- OQ=|3m+8|
- OR=|7−4m|
- OS=∣∣∣3+8m∣∣∣
Topper's Solved these Questions
- THE STRAIGHT LINE BOOK - ICSECHAPTER - THE STRAIGHT LINE EXERCISE - EXERCISE 16 (c)
19 Videos
- THE STRAIGHT LINE BOOK - ICSECHAPTER - THE STRAIGHT LINE EXERCISE - EXERCISE 16 (d)
20 Videos
- THE STRAIGHT LINE BOOK - ICSECHAPTER - THE STRAIGHT LINE EXERCISE - EXERCISE 16 (a)
46 Videos
- STRAIGHT LINES BOOK - ICSECHAPTER - STRAIGHT LINES EXERCISE - Multiple Choice Questions
46 Videos
- TRIGONOMETRIC FUNCTIONBOOK - ICSECHAPTER - TRIGONOMETRIC FUNCTIONEXERCISE - MULTIPLE CHOICE QUESTIONS
44 Videos
Similar Questions
The line 3x - 4y + 12 = 0 meets x-axis at point A and y-axis at point B. Find :
the co-ordinates of A and B.
View SolutionThe line through P(5, 3) intersects y-axis at Q.

Find the co-ordinates of Q.
View SolutionA line AB meets X-axis at A and Y-axis at B. P(4,−1) divides AB in the ratio 1:2.

Find the co-ordinates of A and B.
View SolutionThe line 2x+3y=12 meets the x-axis at A and y-axis at B. The line through (5,5) perpendicular to AB meets the x-axis and the line AB at C and E respectively. If O is the origin of coordinates, find the area of figure OCEB.
View SolutionThe line 4x + 5y + 20 = 0 meets x-axis at point A and y-axis at point B. Find :
the co-ordinates of points A and B.
View SolutionThe equation of a line is 3x−4y+12=0. It meets the x-axis at point A and the y-axis at point B. Find :
the co-ordinates of points A and B.
View SolutionA straight line through the point (1,1) meets the X-axis at A and Y-axis at B. The locus of the mid-point of AB is
View SolutionA line AB meets X-axis at A and Y-axis at B. P(4,−1) divides AB in the ratio 1:2.
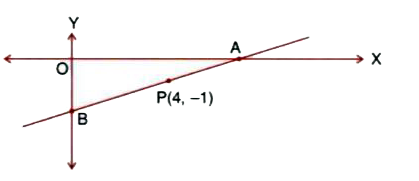
Find the Coordinates of A and B
View SolutionA line AB meets X-axis at A and Y-axis at B. P(4, -1) divides AB in the ratio 1:2.
(i) Find the coordinates of A and B.
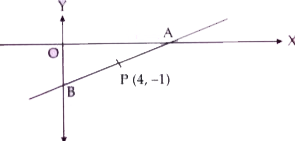
View SolutionThe straight line 2x+3y=24 meets the x-axis at P and the y-axis at Q. The perpendicular bisector of PQ meets the line through (-2,0) parallel to the y-axis at R. Find the area of the ΔPQR.
View Solution
