The locus of the mid-points of the chords of the circle of lines radiÃ¹s r which subtend an angle $\frac{π}{4}$ at any point on the circumference of the circle is a concentric circle with radius equal to

A

$x^{2} + y^{2} = 1$

B

$x^{2} + y^{2} = \frac{27}{4}$

C

$x^{2} + y 6 (2) = \frac{9}{4}$

D

$x^{2} + y^{2} = \frac{3}{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Let P(h,k) be the mid-point of the chord subtending angle $\frac{2 π}{3}$ at the centre.
In $Δ O P A$ , we have
$\frac{cos (π)}{3} = \frac{O P}{O A}$
$\Rightarrow 2 O P = O A$
$\Rightarrow 4 O P^{2} = O A^{2}$
$\Rightarrow 4 (h^{2} + k^{2}) = 9$
$∴$ Locus of (h,k) is $x^{2} + y^{2} = \frac{9}{4}$ .

|

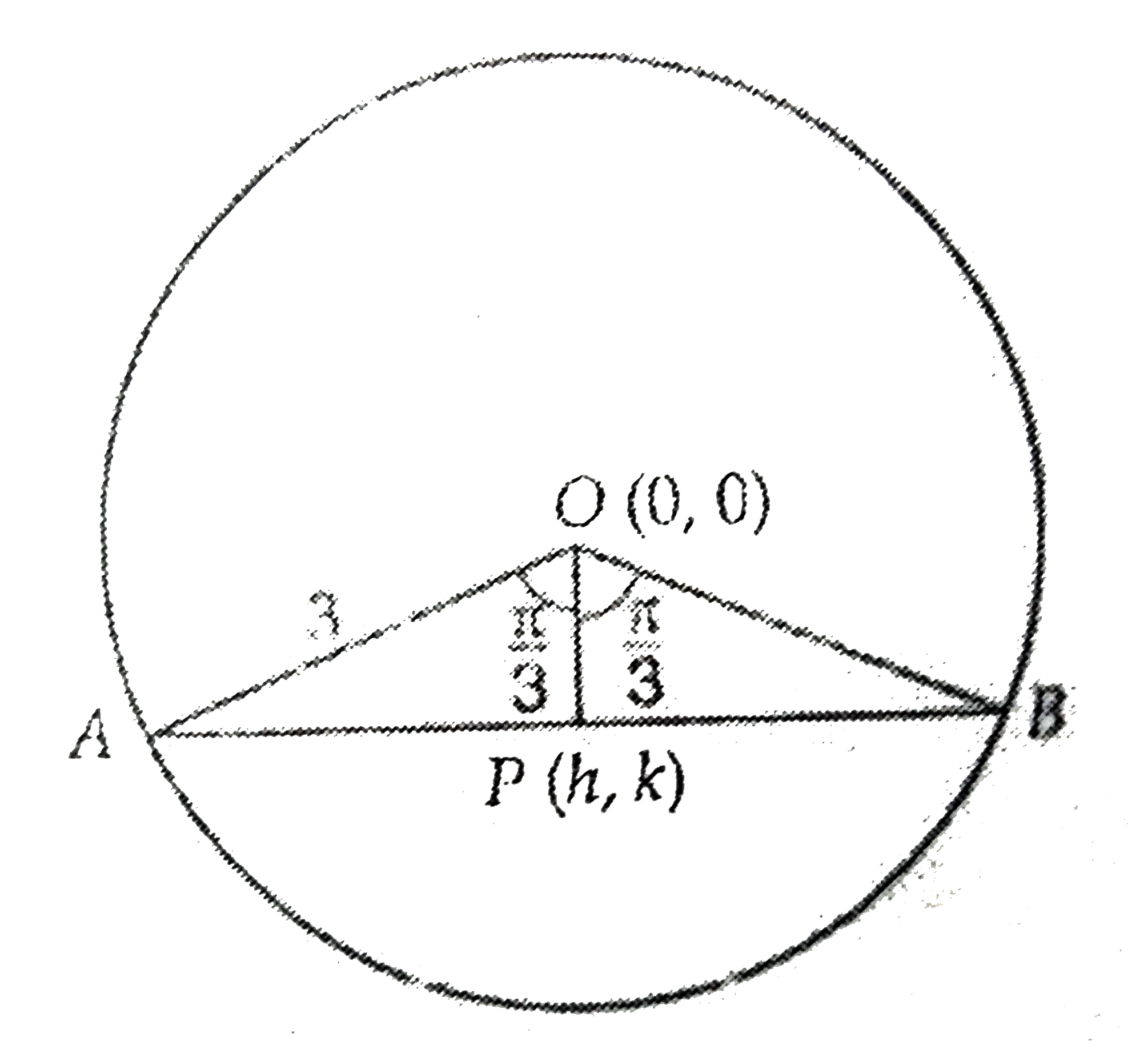
Updated on:21/07/2023

Class 12 MATHS CIRCLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The locus of the mid-points of the chords of the circle $x^{2} + y^{2} + 4 x - 6 y - 12 = 0$ which subtend an angle of $π / 3$ radians at its circumference is
A ${(x + 2)}^{2} + {(y - 3)}^{2} = 6 \cdot 25$
B ${(x - 2)}^{2} + {(y + 3)}^{2} = 6 \cdot 25$
C ${(x + 2)}^{2} + {(y - 3)}^{2} = 18 \cdot 75$
D ${(x + 2)}^{2} + {(y + 3)}^{2} = 18 \cdot 75$
Question 2 - Select One
The locus of the middle points of the chords of the circle $x^{2} + y^{2} = 4 a^{2}$ which subtend a right angle at the centre of the circle is
A $x + y = 2 a$
B $x^{2} + y^{2} = a^{2}$
C $x^{2} + y^{2} = 2 a^{2}$
D $x^{2} + y^{2} = x + y$
Question 3 - Select One
The locus of the mid-points of the chords of the circle $x^{2} + y^{2} - 2 a x - 2 b y = 0$ which subtend a right angle at the centre is
A $a x + b y = 0$
B $a x + b y = a^{2} + b^{2}$
C $x^{2} + y^{2} = a^{2} + b^{2}$
Dnone of these

OBJECTIVE RD SHARMA-CIRCLES-Section I - Solved Mcqs

Home
Ask Doubt
Profile