The locus of the centre of a circle touching the circle x2+y2−4y−2x=2√3−1 internally and tangents on which from (1,2) is making a 60∘ angle with each other is a circle. then integral part of its radius is

A

(x−1)2+(y−2)2=3

B

(x−2)2+(y−1)2=1+2√3

C

x2+y2=1

D

none of these

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:D

Let C2(h,k)be the centre of the circle touching the given circle internally and r be its radius.
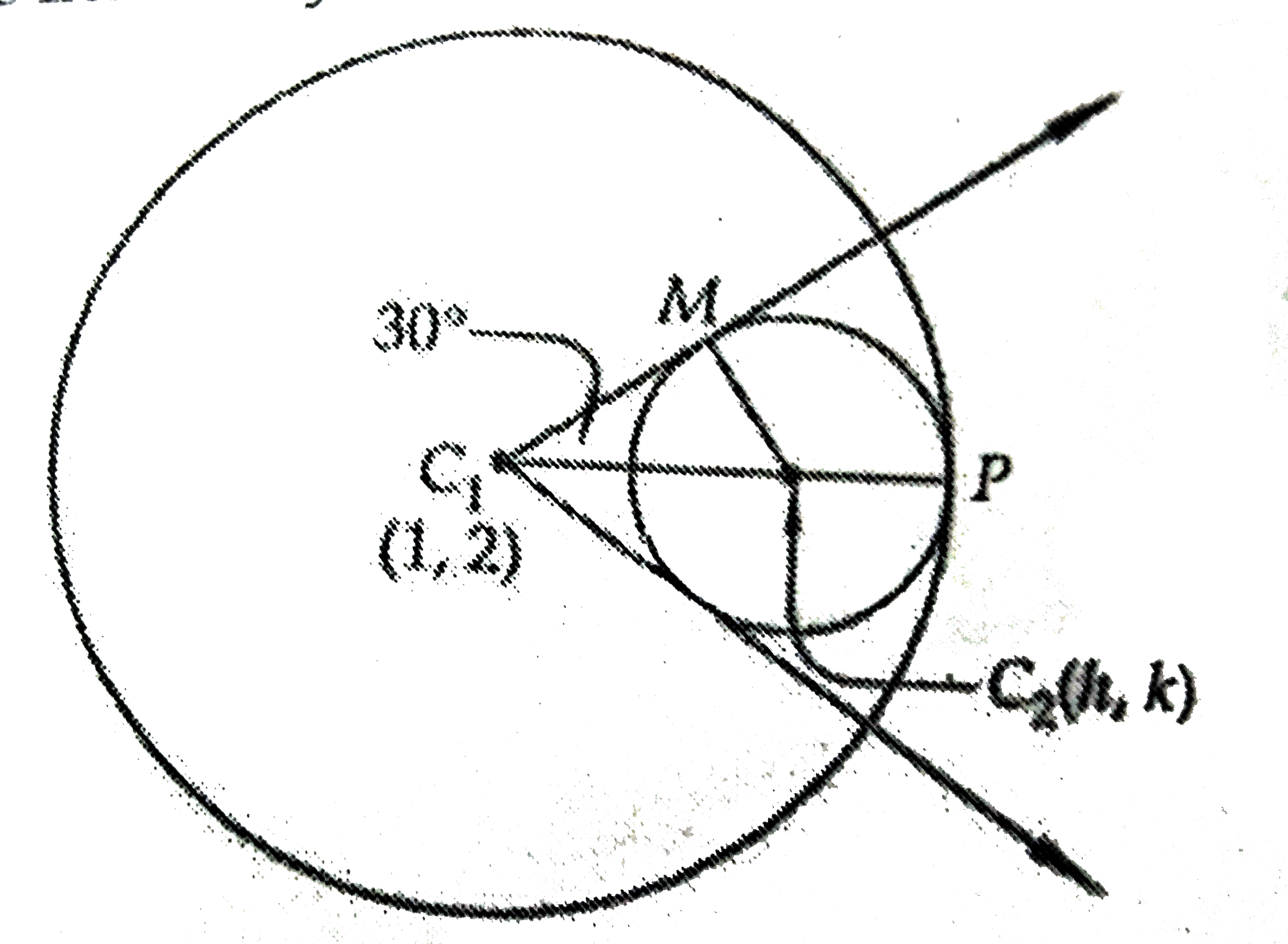
ocr_image
We have,
C1P=√1+4+2√3−1=√4+2√3
Since the circles touch each other internally.
∴C1C2=C1P−C2P
⇒√(h−1)2+(k−2)2=√4+2√3−r
⇒r=√4+2√3−√(h−1)2+(k−2)2
In ΔC1MC2, we have
sin30∘=C2MC1C2
⇒12=√4+2√3−√(h−1)2+(k−2)2√(h−1)2+(k−2)2
⇒3√(h−1)2+(k−2)2=2√4+2√3
⇒9[(h−1)2+(k−2)2]=4(4+2√3)
Hence, the locus of (h, k) is
9[(x−1)2+(y−2)2]=4(4+2√3)

Updated on:21/07/2023
|
Class 12MATHSCIRCLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • The locus of centre of circle which touches the circle x2+y2=1 and y− axis in 1st quadrant is

    Ay2=2x−1
    Bx2+1=2y
    Cy2=2x+1
    Dx2−1=2y

  • The locus of centre of the circle which touches the circle x2+(y−1)2=1 externally and also touches x-axis is

    A{(x,y):x2+(y−1)2=4}∪{(x,y):y<0}
    B{(x,y):x2=4y}∪{(0,y):y<0}
    C{(x,y):x2=y}∪{(0,y):y<0}
    D{(x,y):x2=4y}∪{(x,y):y>0}

  • The locus of centre of the circle which touches the circle x2+(y−1)2=1 externally and also touches x-axis is

    A{(x,y):x2+(y−1)2=4}∪{(x,y):y>0}
    B{(x,y):x2=4y}∪{(0,y):(y<0)}
    C{(x,y):x2=y}∪{(0,y):y<0}
    D{(x,y):x2=4y}∪{(x,y):y<0}