Let $A B C D$ be a quadrilateral with are $18$ , side $A B$ parallel to the side $C D, a n d A B = 2 C D$ . Let $A D$ be perpendicular to $A B a n d C D$ . If a circle is drawn inside the quadrilateral $A B C D$ touching all the sides, then its radius is $3$ (b) 2 (c) $\frac{3}{2}$ (d) 1

A

3

B

2

C

$3 / 2$

D

1

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Let $C D = α$ . Then, AB=2 $α$ .
The equation of BC is
$y = - \frac{2 r}{α} (x - 2 α) or, 2 r x + α y - 4 r α = 0$

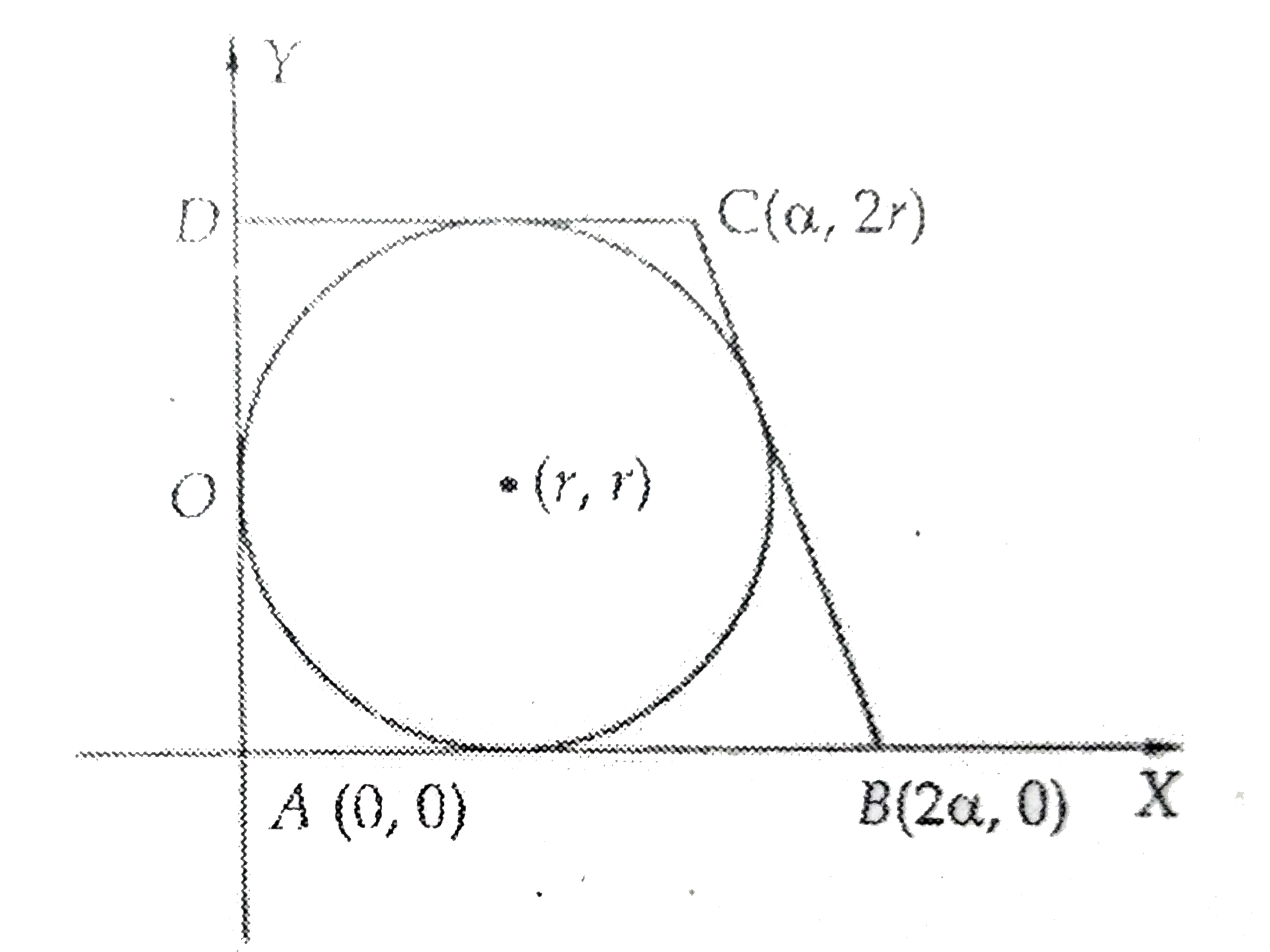
It touches the circle ${(x - 1)}^{2} + {(y - r)}^{2} = r^{2}$
$∴ ∣ ∣ ∣ \frac{2 x^{2} + α r - 4 α r}{\sqrt{4 r^{2} + α^{2}}} ∣ ∣ ∣ = r$
$\Rightarrow {(2 r^{2} - 3 α r)}^{2} = r^{2} (α^{2} + 4 r^{2})$
$\Rightarrow {(2 r - 3 α)}^{2} = (α^{2} + 4 r^{2}) \Rightarrow - 12 r α + 9 α^{2} = α^{2} \Rightarrow α = \frac{3 r}{2}$

Now, Area of quadrilateral ABCD = 18
$\Rightarrow \frac{1}{2} (A B + C D) x 2 r = 18$
$\Rightarrow 3 α r = 18$
$\Rightarrow α r = 6 \Rightarrow 3 r^{2} = 12 [∴ α = \frac{3 r}{2}]$
$\Rightarrow r = 2$

Updated on:21/07/2023

|

Class 12 MATHS CIRCLES

Topper's Solved these Questions

Similar Questions

OBJECTIVE RD SHARMA-CIRCLES-Section I - Solved Mcqs

Home
Ask Doubt
Profile