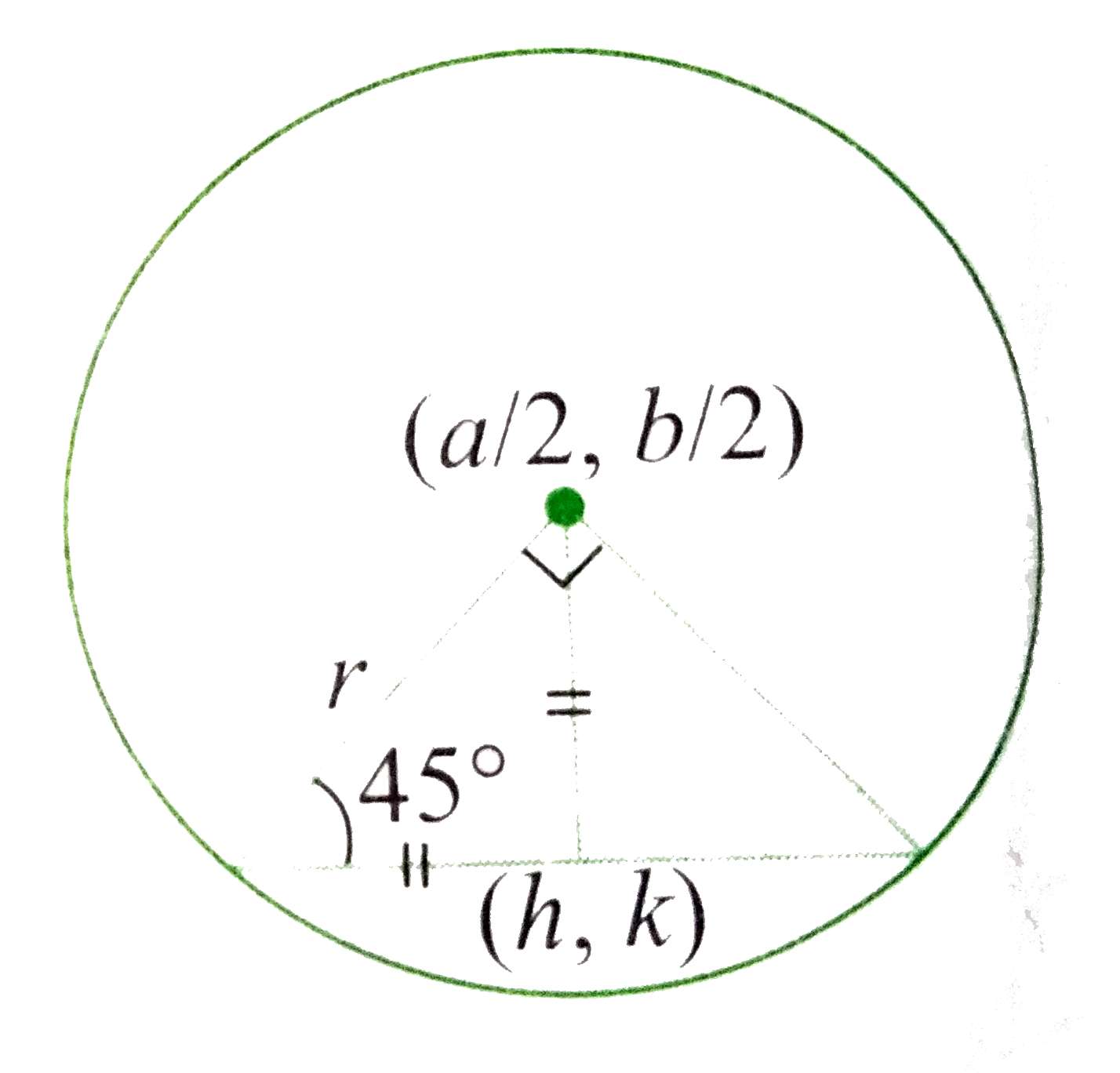
The locus of the midpoints of the chords of the circle x2+y2−ax−by=0 which subtend a right angle at (a2,b2) is (a) ax+by=0 (b) ax+by=a2=b2 (c) x2+y2−ax−by+a2+b28=0 (d) x2+y2−ax−by−a2+b28=0Solution in Tamil
ax+by=0
ax+by=a2=b2
x2+y2−ax−by+a2+b28=0
x2+y2−ax−by−a2+b28=0
The correct Answer is:3
r=√a24+b24=√a2+b22
sin45∘=√(h−a2)2+(h−b2)2√a2+b2/2
or 12=4⎡⎢
⎢⎣(2h−a)24+(2k−b)24a2+b2⎤⎥
⎥⎦
Simplify to get locus x2+y2−ax−by−a2+b28=0
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Multiple)
25 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Comprehension)
46 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise 4.6
5 Videos
- BINOMIAL THEOREMBOOK - CENGAGECHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
16 Videos
Similar Questions
about to only mathematics
View SolutionEach side of a square is of length 6 units and the centre of the square Is ( - 1, 2). One of its diagonals is parallel to x+y=0. Find the co-ordinates of the vertices of the square.
View SolutionIf the circle x2+y2+2x+3y+1=0 cuts x2+y2+4x+3y+2=0 at AandB , then find the equation of the circle on AB as diameter.
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
View SolutionIf the origin is shifted to the point (aba−b,0) without rotation, then the equation (a−b)(x2+y2)−2abx=0 becomes (A)(a−b)(x2+y2)−(a+b)xy+abx=a2 (B)(a+b)(x2+y2)=2ab (C)(x2+y2)=(a2+b2) (D)(a−b)2(x2+y2)=a2b2
View Solution(x)/(a)+(y)/(b)=a+b(x)/(a^(2))+(y)/(b^(2))=2,a!=0,b!=0
View Solutiona2x−b2y=0a2bx+b2ay=a + b, where x, y≠0.
View SolutionSolve the following pair of equations for x and y :
a2x−b2y=0,a2bx+b2ay=a+b,
x≠0,y≠0.
View SolutionThe image of the pair of lines represented by ax2+2hxy+by2=0 by the line mirror y=0 is ax2−2hxy−by2=0 bx2−2hxy+ay2=0 bx2+2hxy+ay2=0 ax2−2hxy+by2=0
View SolutionIf the origin is shifted to the point (aba−b,0) without rotation, then the equation (a−b)(x2+y2)−2abx=0 becomes
View SolutionThe image of the pair of lines represented by ax2+2hxy+by2=0 by the line mirror y=0 is ax2−2hxy−by2=0 bx2−2hxy+ay2=0 bx2+2hxy+ay2=0 ax2−2hxy+by2=0
View SolutionThe locus of the midpoints of the chords of the circle x2+y2−ax−by=0 which subtend a right angle at (a2,b2) is (a)ax+by=0 (b) ax+by=a2+b2 (c) x2+y2−ax−by+a2+b28=0 (d) x2+y2−ax−by−a2+b28=0
View SolutionSolve : a(x+y)+b(x−y)=a2−ab+b2, a(x+y)−b(x−y)=a2+ab−b2
View SolutionEquation of the circle through origin which cuts intercepts of length a and b on axes is a. x2+y2=ax+by=0 b. x2+y2−ax−by=0 c. x2+y2+bx+ay=0 d. none of these
View SolutionFactorize: ax+bx+ay+by, ax2+by2+bx2+ay2, a2+bc+ab+ac, ax−ay+bx−by
View Solution
