The medians of a triangle ABC intersect each other at point G. If one of its medians is AD, Prove that :
(i)
(ii)
(iii)
To solve the problem, we will prove the three statements step by step.
Step 1: Understanding the Triangle and Medians
Let triangle ABC be given, with medians AD, BE, and CF intersecting at point G (the centroid). The centroid divides each median in the ratio 2:1.
Step 2: Proving (i) Area(ΔABD) = 3 × Area(ΔBGD)
1. Identify Areas:
- Let Area(ΔBGD) = x.
- Since G divides AD in the ratio 2:1, Area(ΔBGA) will be twice that of Area(ΔBGD).
- Therefore, Area(ΔBGA) = 2x.
2. Calculate Area(ΔABD):
- Area(ΔABD) = Area(ΔBGA) + Area(ΔBGD) = 2x + x = 3x.
3. Conclusion:
- Thus, Area(ΔABD) = 3 × Area(ΔBGD).
Step 3: Proving (ii) Area(ΔACD) = 3 × Area(ΔCGD)
1. Identify Areas:
- Let Area(ΔCGD) = y.
- By the same reasoning, Area(ΔCGA) will be twice that of Area(ΔCGD).
- Therefore, Area(ΔCGA) = 2y.
2. Calculate Area(ΔACD):
- Area(ΔACD) = Area(ΔCGA) + Area(ΔCGD) = 2y + y = 3y.
3. Conclusion:
- Thus, Area(ΔACD) = 3 × Area(ΔCGD).
Step 4: Proving (iii) Area(ΔBGC) = (1/3) × Area(ΔABC)
1. Combine Areas:
- From the previous parts, we have:
- Area(ΔABD) = 3 × Area(ΔBGD) = 3x
- Area(ΔACD) = 3 × Area(ΔCGD) = 3y
2. Total Area of Triangle ABC:
- Area(ΔABC) = Area(ΔABD) + Area(ΔACD) + Area(ΔBGC).
- Let Area(ΔBGC) = z.
3. Express Total Area:
- Area(ΔABC) = 3x + 3y + z.
4. Relate Areas:
- Since G is the centroid, it divides the triangle into three triangles of equal area. Thus, Area(ΔBGC) = Area(ΔBGD) + Area(ΔCGD) = x + y.
- Therefore, Area(ΔABC) = 3x + 3y + (x + y) = 4x + 4y.
5. Final Calculation:
- Since Area(ΔBGC) = (1/3) × Area(ΔABC), we can express Area(ΔABC) as 3 × Area(ΔBGC).
Conclusion
Thus, we have proved:
1. Area(ΔABD) = 3 × Area(ΔBGD)
2. Area(ΔACD) = 3 × Area(ΔCGD)
3. Area(ΔBGC) = (1/3) × Area(ΔABC)
Let triangle ABC be given, with medians AD, BE, and CF intersecting at point G (the centroid). The centroid divides each median in the ratio 2:1.
- Let Area(ΔBGD) = x.
- Since G divides AD in the ratio 2:1, Area(ΔBGA) will be twice that of Area(ΔBGD).
- Therefore, Area(ΔBGA) = 2x.
- Area(ΔABD) = Area(ΔBGA) + Area(ΔBGD) = 2x + x = 3x.
- Thus, Area(ΔABD) = 3 × Area(ΔBGD).
- Let Area(ΔCGD) = y.
- By the same reasoning, Area(ΔCGA) will be twice that of Area(ΔCGD).
- Therefore, Area(ΔCGA) = 2y.
- Area(ΔACD) = Area(ΔCGA) + Area(ΔCGD) = 2y + y = 3y.
- Thus, Area(ΔACD) = 3 × Area(ΔCGD).
- From the previous parts, we have:
- Area(ΔABD) = 3 × Area(ΔBGD) = 3x
- Area(ΔACD) = 3 × Area(ΔCGD) = 3y
- Area(ΔABC) = Area(ΔABD) + Area(ΔACD) + Area(ΔBGC).
- Let Area(ΔBGC) = z.
- Area(ΔABC) = 3x + 3y + z.
- Since G is the centroid, it divides the triangle into three triangles of equal area. Thus, Area(ΔBGC) = Area(ΔBGD) + Area(ΔCGD) = x + y.
- Therefore, Area(ΔABC) = 3x + 3y + (x + y) = 4x + 4y.
- Since Area(ΔBGC) = (1/3) × Area(ΔABC), we can express Area(ΔABC) as 3 × Area(ΔBGC).
Thus, we have proved:
1. Area(ΔABD) = 3 × Area(ΔBGD)
2. Area(ΔACD) = 3 × Area(ΔCGD)
3. Area(ΔBGC) = (1/3) × Area(ΔABC)
Topper's Solved these Questions
- AREA THEOREMSBOOK - ICSECHAPTER - AREA THEOREMSEXERCISE - Exercies 16(B)
16 Videos
- AREA AND PERIMETER OF PLANE FIGURESBOOK - ICSECHAPTER - AREA AND PERIMETER OF PLANE FIGURESEXERCISE - EXERCISE 20(D)
12 Videos
- CHAPTER REVISION (STAGE 2) BOOK - ICSECHAPTER - CHAPTER REVISION (STAGE 2) EXERCISE - DISTANCE FORMULA
12 Videos
Similar Questions
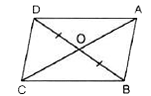
In the given figure, the diagonals AC and BD intersects at point O. If OB=OD and AB//DC, prove that :
(i) Area(ΔDOC)=Area(ΔAOB).
(ii) Area(ΔDCB)=Area(ΔACB).
(iii) ABCD is a parallelogram.
View SolutionThe medians of ΔABC intersect at point G. Prove that:
area of ΔAGB=13× area of ΔABC
View SolutionThe median BE and CF of a triangle ABC intersect at G. Prove that the area of ΔGBC= area of the quadrilateral AFGE.
View SolutionThe medians BE and CF of a triangle ABC intersect at G . Prove that area of △GBC=area of quadrilateral AGFE.
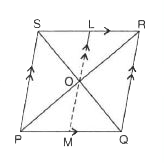
View SolutionIn the given figure, diagonals PR and QS of thr parallelogram PQRS intersect at point O and LM is parallel to PS. Show that :
(i) 2Area(ΔPOS)=Area(//gmPMLS)
(ii) Area(ΔPOS)+Area(ΔQOR)
=12Area(//gmPQRS)
(iii) Area(ΔPOS)+Area(ΔQOR)
=Area(ΔPOQ)+Area(tΔSOR)
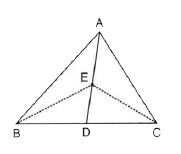
View SolutionIn the given figure, AD is median of ΔABC and E is any point on median AD. Prove that Area (ΔABE) = Area (ΔACE)
View SolutionIn the figure of question 2, if E is the mid point of median AD, then prove that :
Area(ΔABE)=14Area(ΔABC).
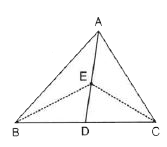
View SolutionIn the figure of question 2, if E is the mid point of median AD, then prove that :
Area(ΔABE)=14Area(ΔABC).

View SolutionD is the mid-point of side AB of the triangle ABC.E is the mid-point of CD and F is the mid-point of AE. Prove that 8× area of (ΔAFD)= area of ΔABC
View SolutionIn triangle ABC, D is a point in side BC such that 2BD=3DC. Prove that the area of triangle ABD = 35×Area ofΔABC
View Solution
