The median BE and CF of a triangle ABC intersect at G. Prove that the area of area of the quadrilateral AFGE.
Given In , medians BE and CF intersect each other at G. To prove
Proof Since, BE is the median of and we know that a median of a triangle divides it into two parts of equal area.
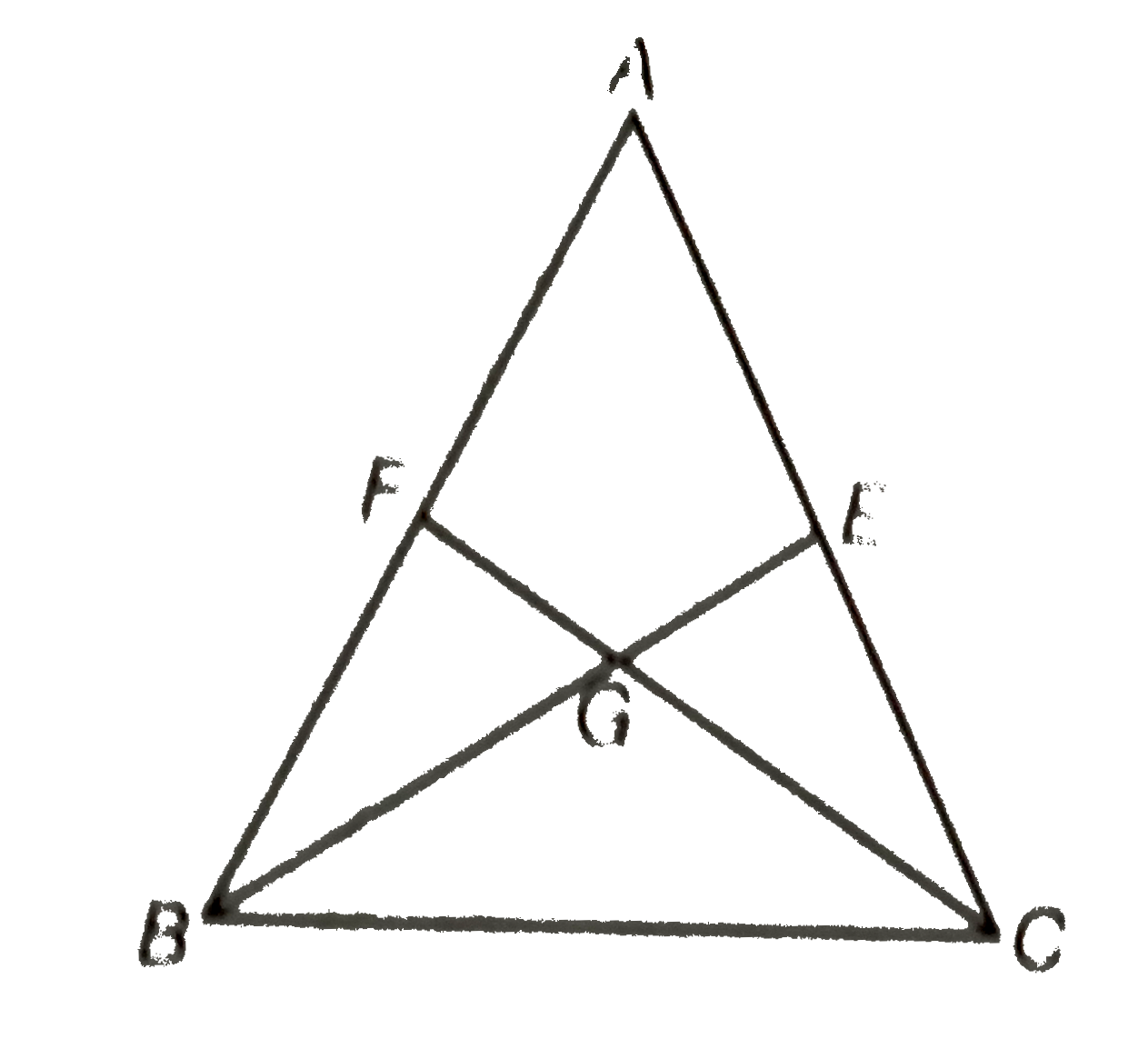
So,
...(i)
Similarly, CF is the median of .
Then,
...(ii)
From Eqs. (i) and (ii),
...(iii)
On substracting from both sides of Eq. (iii), we get
Hence proved.
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the figure, what is the area of ΔABC?
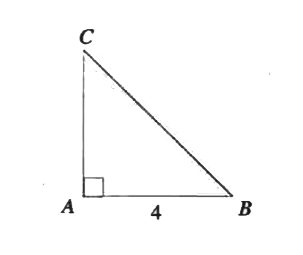 A6B7C8DIt cannot be determined from the information given
A6B7C8DIt cannot be determined from the information givenIn the figure, what is the area of ΔABC?
 A2B√2C1D1/2
A2B√2C1D1/2
The medians of ΔABC intersect at point G. Prove that:
area of ΔAGB=13× area of ΔABC
View SolutionIn the figure, given below, the medians BD and CE of a triangle ABC meet at G. Prove that:
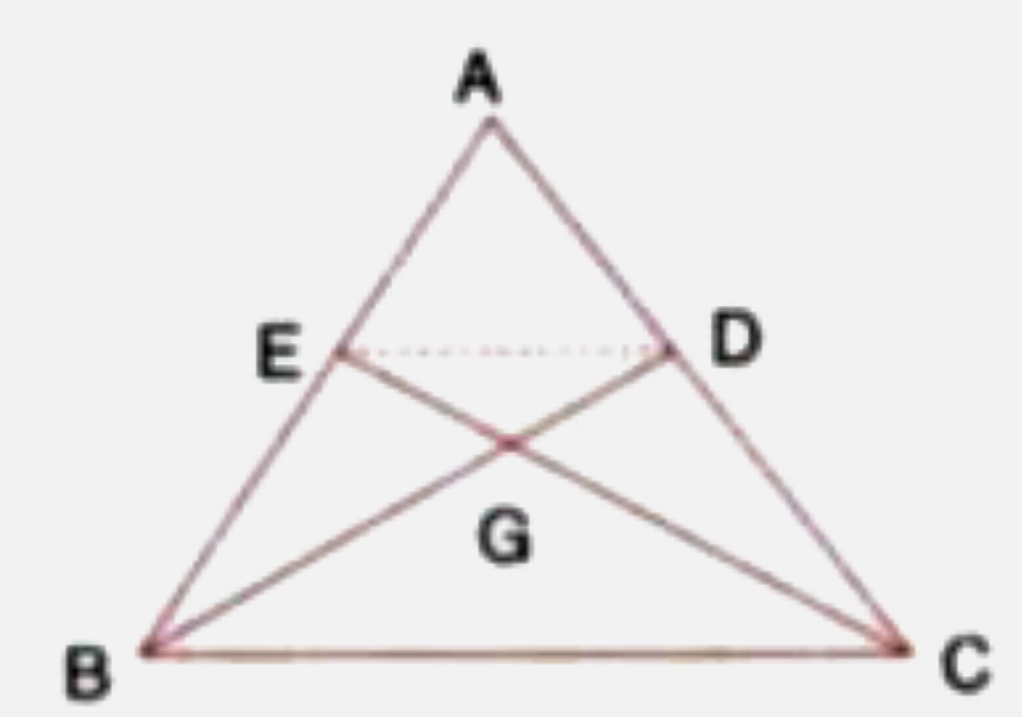
ΔEGD−ΔCGBand (ii) BG=2GD from (i) above.
View SolutionThe base BC of triangle ABC is divided at D so that BD = 12 DC.
Prove that area of ΔABD=13 of the area of ΔABC.
View SolutionABC is a right angled triangle with ∠ABC=90∘, D is any point on AB and DE is perpendicular to AC. Prove that :
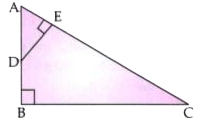
(iii) Find area of Δ ADE : area of quadrilateral BCED.If AC = 13 cm, BC = 5 cm and AE = 4 cm.
View SolutionABC is a right angled triangle with ABC=90∘. D is any point on AB and DE is perpendicular to AC. Prove that:

Find, area of AADE: area of quadrilateral BCED.
View SolutionIn the adjoining figure, ABCD is a quadrilateral in which AD∣∣BC. AC and BD intersect each other at point 'O'. Prove that:
area of ΔCOD= area of ΔABO
View Solution
