The number of function f:[0,1]→[0,1] satisfying |f(x)−f(x)|=|x−y| for all x,y in [0,1]is
A
exactly 1
B
exactly 2
C
more than 2 but finite
D
inifinite
Video Solution
Text Solution
The correct Answer is:B
|f(x)=f(x)|=|x−y|
⇒|f(x)=f(x)||x−y|=1
Take limx→y|f'(x)|=1
⇒f'(x)=±1
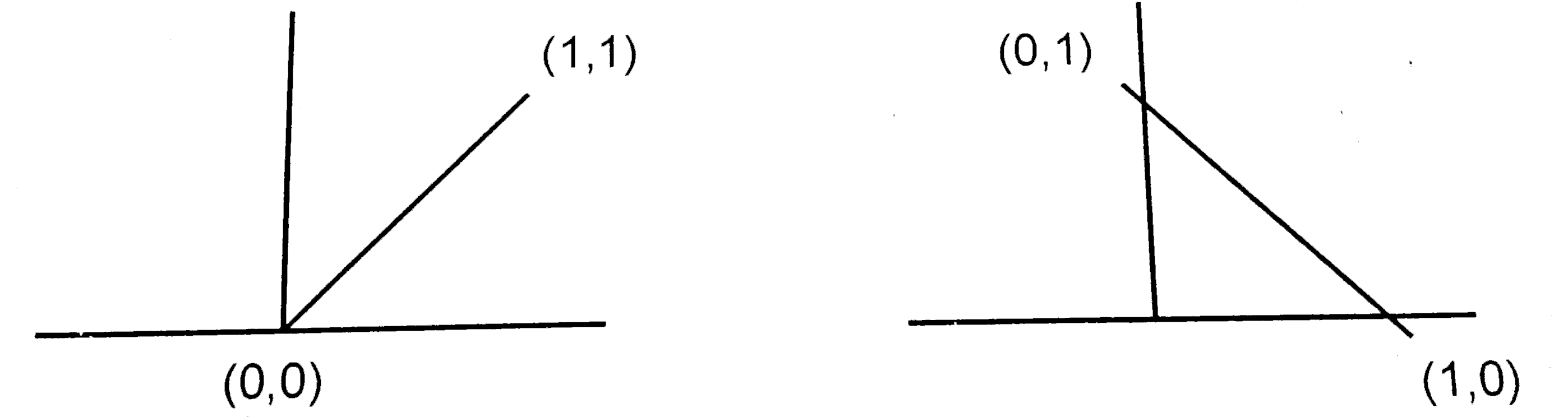
Hence two function possible
|
Topper's Solved these Questions
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - PART-2 MATHMATICS
10 Videos
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - Part 2 Mathematics
15 Videos
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - Part B- Mathematics
10 Videos
- KVPY 2021BOOK - KVPY PREVIOUS YEARCHAPTER - KVPY 2021EXERCISE - PART II MATHEMATICS
4 Videos
Similar Questions
Knowledge Check
Let f:[0,1]→R be an injective continuous function that satisfies the condition −1<f(0)<f(1)<1
Then the number of functions g:[−1,1]→[0,1] such that (gof)x=x for all x∈[0,1] isA0B1Cmore than 1, but finiteDinfiniteLet f be a continuous function on R satisfying f(x+y)=f(x)+f(y) for all x,y∈R with f(1)=2andg be a function satisfying f(x)+g(x)=ex then the value of the integral ∫10f(x)g(x)dx is
A1e−4B14(e−2)C2/3D12(e−3)Le the be a real valued functions satisfying f(x+1)+f(x−1)=2f(x) for all x,y∈R and f(0)=0, then for any n∈N, f(n) =
An f(1)B[f(1)]nC0Dnone of these
There exists a function f(x) satisfying
f{0}=1,f'{0}=−1,f(x)>0 for all x and
View SolutionLet f be differentiable function satisfying f(xy)=f(x)−f(y)for allx,y>0. If f'(1) = 1, then f(x) is
View SolutionLet f:[0,1] → R be a function . Suppose the fuction f is twice differentiable with f(0) =f(1)=0 and satisfies
f(x)−2f(x)+f(x)≥ex for all x∈[0,1].Which of the following is true for x ∈(0,1] ?
View SolutionLet f be a real valued function, satisfying f(x+y)=f(x)f(y) for all a,y ∈R Such that,f(1=a.Then,f(x)=
View SolutionLet f (x) be a function satisfying f(x+y)=f(x)f(y) for all x,y∈R and f(x)=1+xg(x) where limx→0g(x)=1 then f'(x) is equal to
View Solution
