The number of pairs (a, b) of positive real numbers satisfying is
0
1
2
more than 2
The correct Answer is:D
Let
Now given condition is
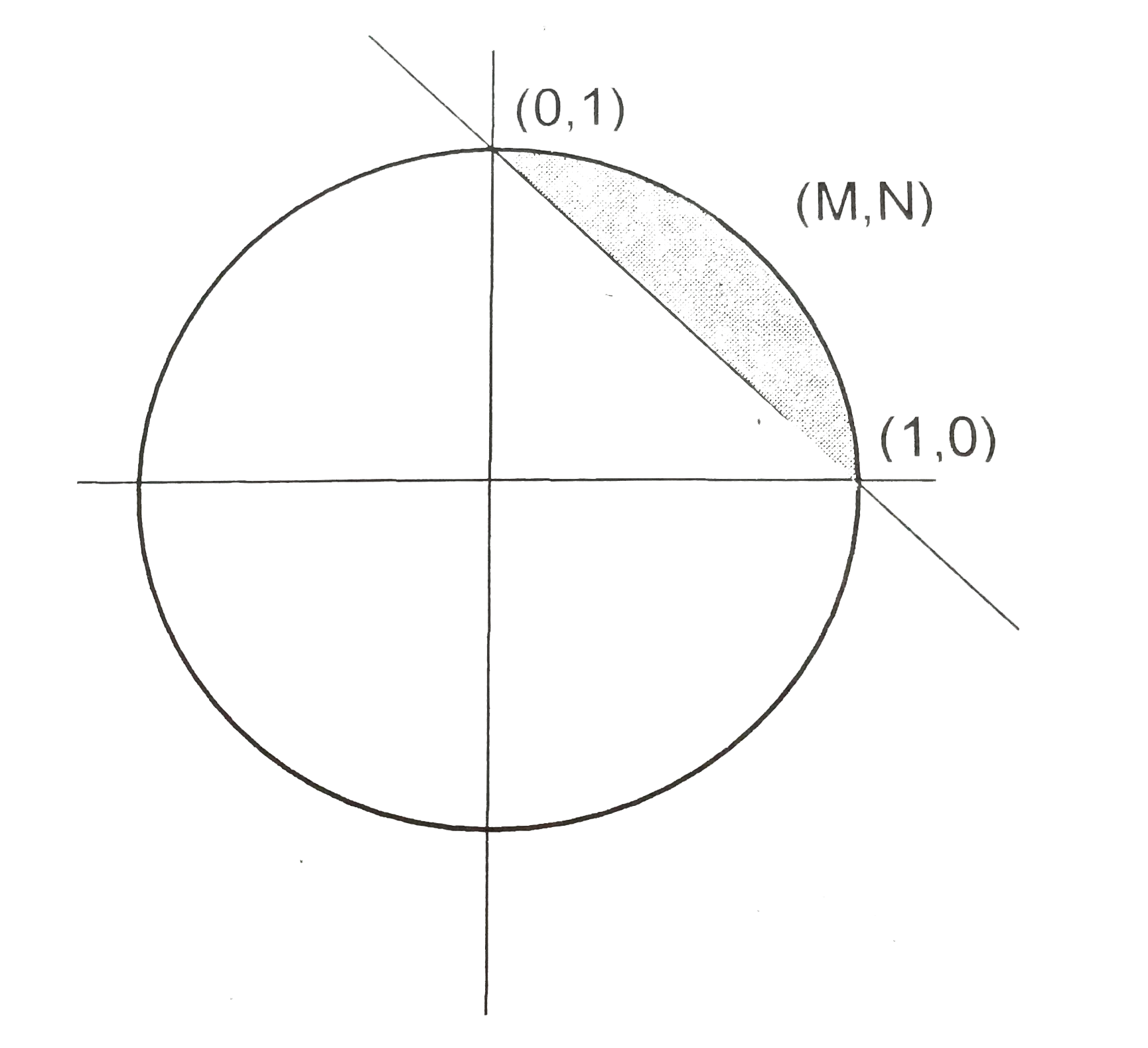
(M,N) lies inside circle
lies shaded region and number of points in shaded refion are infinite, so number of pair (a, b) are also infinite.
Topper's Solved these Questions
Similar Questions
If 2a=7b then number of ordered pairs (a,b) of real numbers is
View SolutionThe number of ordered pairs (a,b) of positive integers such that2a−1b and 2b−1a are both integers is
View SolutionLet a and b be positive real numbers with a3+b3=a−bandk=a2+4b2 , then (1)k<1 (2) k>1 (3) k=1(4) k>2
View SolutionThe number of ordered pairs (a,b) where a,b are integers satisfying the inequality min (x2+(a−b)x+(1−a−b))>max(−x2+(a+b)x−(1+a+b)∀x∈R, is :
View SolutionLet a>0,a≠0. Then the set S of all positive real numbers b satisfying (1+a2)(1+b2)=4ab is
View Solutiona≠0,b≠0. The number of real number pair (a, b) which satisfy the equation a4+b4=(a+b)4 is:
View SolutionThe number of positive integral pairs satisfying the equation tan−1a+tan−1b=tan−13
View SolutionFind the number of ordered pair of real numbers (x, y) satisfying the equation:
5x(1+1x2+y2)=12&5y(1−1x2+y2)=4
View SolutionIf a and b are positive real numbers such that a2b3=49,then least value of a+b is
View SolutionSuppose that a b c d are real numbers satisfying a≥b≥c≥d≥0 a2+d2=1andb2+c2=1 and ac+bd=13 .The value of ab-cd is
View Solution
