The percentage of marks obtained by a student in six units tests are given below:
∣∣∣Unit testIIIIIIIVVVI5% of marks obtained537228466759∣∣∣
A unit test is selected at random. What is the probability that the student gets more than 60% marks in the test.
The correct Answer is:13
To solve the problem, we need to find the probability that a student gets more than 60% marks in a randomly selected unit test.
1. Identify the Marks Obtained:
The marks obtained by the student in the six unit tests are:
- Unit Test I: 53%
- Unit Test II: 72%
- Unit Test III: 28%
- Unit Test IV: 46%
- Unit Test V: 67%
- Unit Test VI: 59%
2. Determine the Total Number of Unit Tests:
There are a total of 6 unit tests.
3. Identify Favorable Outcomes:
We need to find out how many of these tests have marks greater than 60%.
- Unit Test I: 53% (not favorable)
- Unit Test II: 72% (favorable)
- Unit Test III: 28% (not favorable)
- Unit Test IV: 46% (not favorable)
- Unit Test V: 67% (favorable)
- Unit Test VI: 59% (not favorable)
The favorable outcomes (tests with more than 60%) are Unit Test II and Unit Test V. Therefore, there are 2 favorable outcomes.
4. Calculate the Probability:
The probability (P) is given by the formula:
P=Number of Favorable OutcomesTotal Number of Outcomes
Substituting the values we found:
P=26=13
5. Conclusion:
The probability that the student gets more than 60% marks in a randomly selected unit test is 13.
The marks obtained by the student in the six unit tests are:
- Unit Test I: 53%
- Unit Test II: 72%
- Unit Test III: 28%
- Unit Test IV: 46%
- Unit Test V: 67%
- Unit Test VI: 59%
There are a total of 6 unit tests.
We need to find out how many of these tests have marks greater than 60%.
- Unit Test I: 53% (not favorable)
- Unit Test II: 72% (favorable)
- Unit Test III: 28% (not favorable)
- Unit Test IV: 46% (not favorable)
- Unit Test V: 67% (favorable)
- Unit Test VI: 59% (not favorable)
The probability (P) is given by the formula:
P=Number of Favorable OutcomesTotal Number of Outcomes
Substituting the values we found:
P=26=13
The probability that the student gets more than 60% marks in a randomly selected unit test is 13.
Topper's Solved these Questions
- PROBABILITYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - PROBABILITYEXERCISE - Revision Exercise (very Short Answer /short Answer Questions)
10 Videos
- PROBABILITYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - PROBABILITYEXERCISE - Problems From NCERT/exemplar
7 Videos
- POLYNOMIALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - POLYNOMIALSEXERCISE - Revision Exercise (short Answer Questions)
16 Videos
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Revision Exercise (long Answer Questions)
5 Videos
Similar Questions
The percentage of marks obtained by a student in the monthly unit tests are given below.Based on this data, find the probability that the student gets more than 70% marks in a unit test.
View SolutionThe percentage of marks obtained by a student in the monthly unit tests are given below: Unit test: I II III IV V Percentage of marks obtained: 58 74 76 62 85 Find the probability that the student gets: (i) a first class i.e. at least 60% marks (ii) marks between 70% and 80% (iii) a distinction i.e. 75% or above (iv) less than 65% marks.
View SolutionThe percentage of marks obtained by a student in monthly unit tests are given below: Unit I II III IV V Percentage of marks obtained 69 71 73 68 76 Find the probability that the student gets: (i) more than 70% marks (ii) less than 70% marks (iii) a distinction
View SolutionThe percentage of marks obtained by a student in different subjects are given below.
SubjectHindiScienceEnglishMathematicsSocial StudiesPercentage of3560157540marks obtained
Draw a bar graph representing the above data.
View SolutionThe marks obtained by 120 students in a Mathematics test are given below:
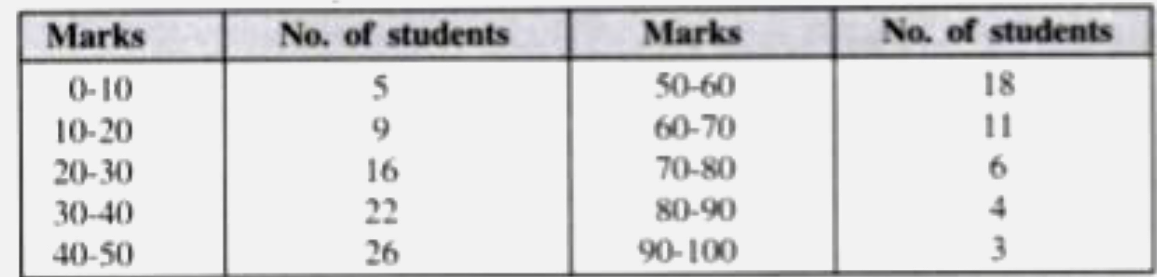
Using the informations, given above, draw an ogive on a graph sheet. Take a suitable scale for your ogive. Use the ogive drawn to estimate :
(i) the median.
(ii) the number of students who obtained more than 75% marks in the test.
(iii) the number of students who did not pass in the test if the pass percentage was 40.
View SolutionUse graph paper for this question.
The marks obtained by 120 students in an English test are given below :
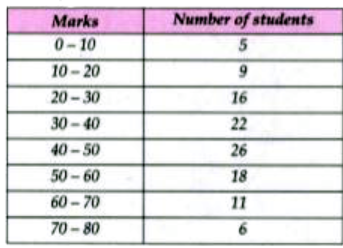

Draw the ogive and hence, estimate :
the median marks.
View SolutionThe marks obtained by 100 students in a Mathematics test are given below :

Draw an ogive for the given distribution on a graph sheet.
(Use a scale of 2 cm = 10 units on both axis).
Use the ogive to estimate the number of students who obtained more than 85% marks in the test.
View SolutionThe frequency distribution of marks obtained by 28 students in a test carrying 40 marks is given below:
Marks:0−1010−2020−3030−40Number of students:6xy6
If the mean of the above data is 20, then the difference between x and y is
View SolutionMarks scored by 100 students in a 25 marks unit test of Mathematics is given below. Their median is
Marks 0−55−1010−1515−2020−25Students 10 18 42 23 7
View SolutionThe frequency distribution of the marks obtained by 100 students in a test carrying 50 marks is given below. Then the mean is
Marks 0−910−1920−2930−3940−49No. of students 8 15 20 45 12
View Solution
