The perpendicular from the centre of a circle to a chord bisects the chord.
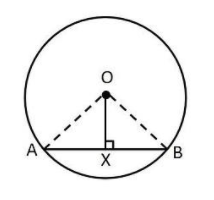
In △OXA and △OXB,
∠OXA=∠OXB (perpendicular angles)
OA=OB (Radius)
OX≡OX (Common)
By RHS rule, △OXA and △OXB are congruent.
AX=BX (CPCT)
Topper's Solved these Questions
- BOOK - NCERT ENGLISHCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 10.41videos
NCERT THEOREMS
- BOOK - NCERT ENGLISHCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 10.51videos
NCERT THEOREMS
- BOOK - NCERT ENGLISHCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 10.21videos
NCERT THEOREMS
- BOOK - NCERT ENGLISHCHAPTER - LINES AND ANGLESEXERCISE - Exercise 6.16videos
LINES AND ANGLES
- BOOK - NCERT ENGLISHCHAPTER - NUMBER SYSTEMSEXERCISE - EXERCISE 1.42videos
NUMBER SYSTEMS
Similar Questions
The radius of a circle is 17-0 cm and the length of perpendicular drawn from its centre to a chord is 8 0 cm. Calculate the length of the chord.
View SolutionWhich of the following statements are true and which have are false? In each case give a valid reason for saying so p: Each radius of as circle is a chord of the circle q: The centre of a circle bisects each chord of the circle.
View Solution
Knowledge Check
- Question 1 - Select One
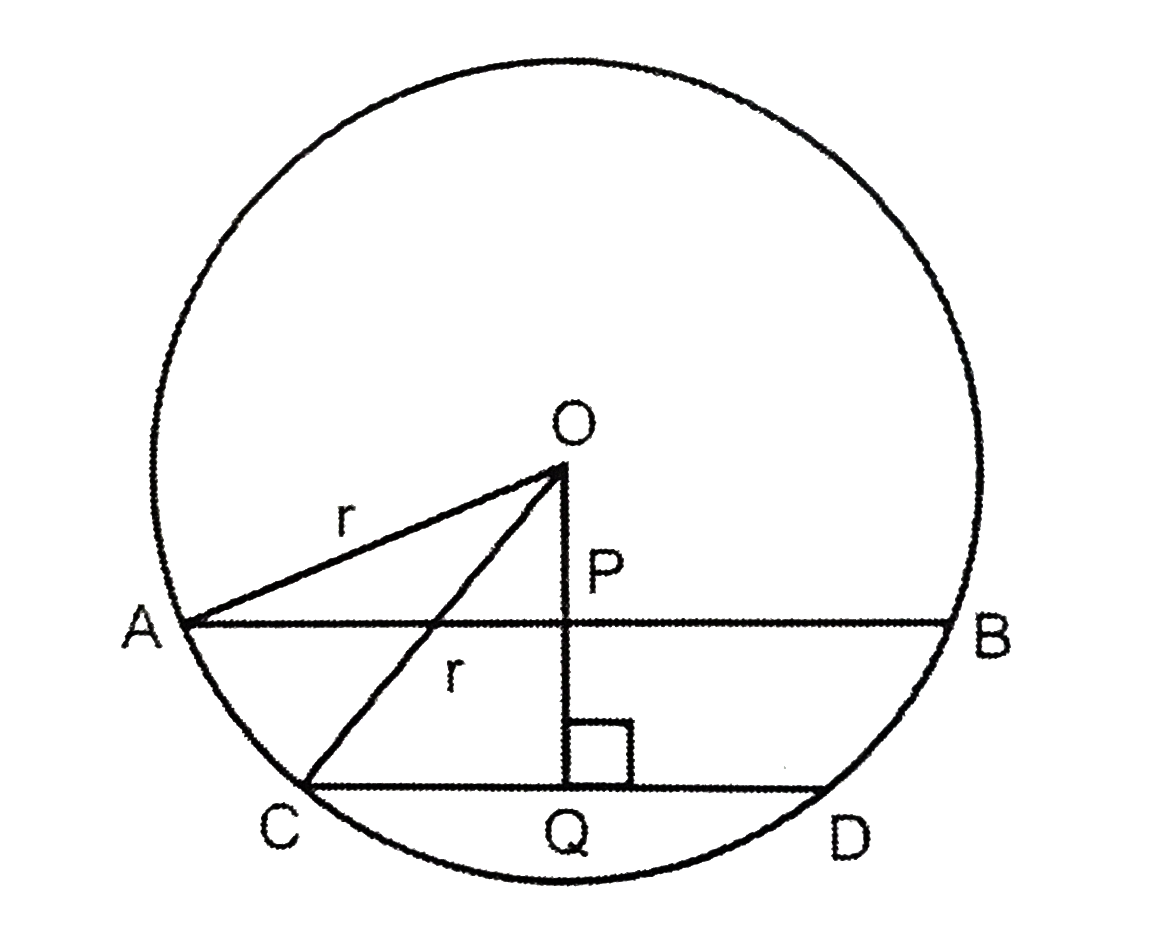
2 parallel chords 24 cm, and 18 cm, are on the same side of the centre of a circle. If the distance between the chords is 3 cm, calculate the radius of the circle.A15 cmB14 cmC13 cmD12 cm - Question 2 - Select One
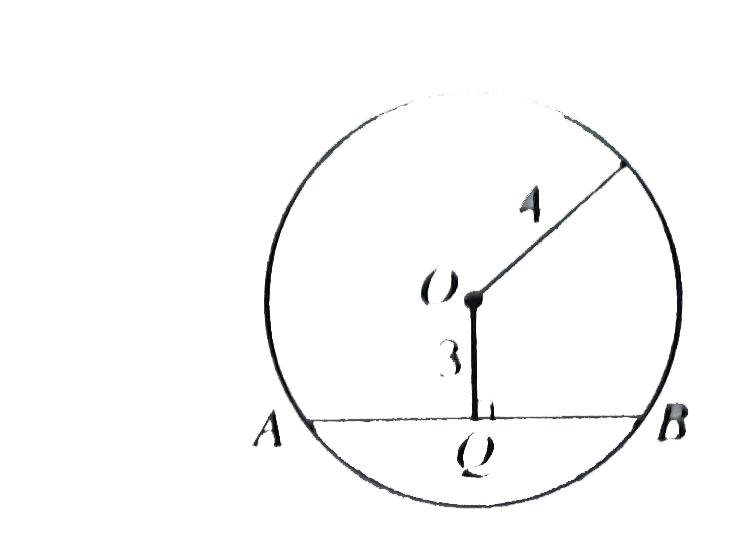
A chord ¯¯¯¯¯¯AB is 3 cm. from the center of a circle with radius 4. What is the length of chord ¯¯¯¯¯¯AB ?A√7B2√7C5D10
A chord of length 8 cm is drawn at a distance of 3 cm from the centre of a circle. Calculate the radius of the circle.
View SolutionFind the length of a chord which is at a distance of 5 cm from the centre of a circle of radius 10 cm.
View SolutionFind the length of a chord which is at a distance of 5 cm from the centre of a circle of radius 13 cm.
View Solution(Converse of Theorem 3) The line joining the centre of a circle to the mid-point of a chord is perpendicular to the chord.
View SolutionProve that the perpendicular bisector of a chord of a circle always passes through the centre.
View SolutionProve that the perpendicular bisector of a chord of a circle always passes through the centre.
View Solution

