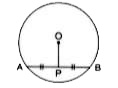
(Converse of Theorem 3) The line joining the centre of a circle to the mid-point of a chord is perpendicular to the chord.
To prove that the line joining the center of a circle to the midpoint of a chord is perpendicular to the chord, we will follow these steps:
Step 1: Define the Elements
Let O be the center of the circle, P and Q be the endpoints of the chord, and M be the midpoint of the chord PQ.
Step 2: Identify the Radii
Since OP and OQ are radii of the circle, we have:
OP=OQ
Step 3: Establish the Midpoint
Since M is the midpoint of chord PQ, we have:
PM=MQ
Step 4: Common Segment
The segment OM is common to both triangles OPM and OQM:
OM=OM
Step 5: Congruent Triangles
Now we can apply the Side-Side-Side (SSS) congruence criterion. We have:
- OP=OQ (radii of the circle)
- PM=MQ (since M is the midpoint)
- OM=OM (common side)
Thus, triangles OPM and OQM are congruent:
△OPM≅△OQM
Step 6: Corresponding Angles
Since the triangles are congruent, the corresponding angles are equal:
∠OPM=∠OQM
Step 7: Sum of Angles
The angles OPM and OQM are supplementary, meaning:
∠OPM+∠OQM=180∘
Step 8: Solve for Angles
Let ∠OPM=x. Then:
x+x=180∘
2x=180∘
x=90∘
Step 9: Conclusion
Thus, we have:
∠OPM=90∘
This means that the line OM is perpendicular to the chord PQ.
Final Statement
Therefore, we have proved that the line joining the center of a circle to the midpoint of a chord is perpendicular to the chord.
---
Let O be the center of the circle, P and Q be the endpoints of the chord, and M be the midpoint of the chord PQ.
Since OP and OQ are radii of the circle, we have:
OP=OQ
Since M is the midpoint of chord PQ, we have:
PM=MQ
The segment OM is common to both triangles OPM and OQM:
OM=OM
Now we can apply the Side-Side-Side (SSS) congruence criterion. We have:
- OP=OQ (radii of the circle)
- PM=MQ (since M is the midpoint)
- OM=OM (common side)
△OPM≅△OQM
Since the triangles are congruent, the corresponding angles are equal:
∠OPM=∠OQM
The angles OPM and OQM are supplementary, meaning:
∠OPM+∠OQM=180∘
Let ∠OPM=x. Then:
x+x=180∘
2x=180∘
x=90∘
Thus, we have:
∠OPM=90∘
This means that the line OM is perpendicular to the chord PQ.
Therefore, we have proved that the line joining the center of a circle to the midpoint of a chord is perpendicular to the chord.
Topper's Solved these Questions
Similar Questions
Knowledge Check
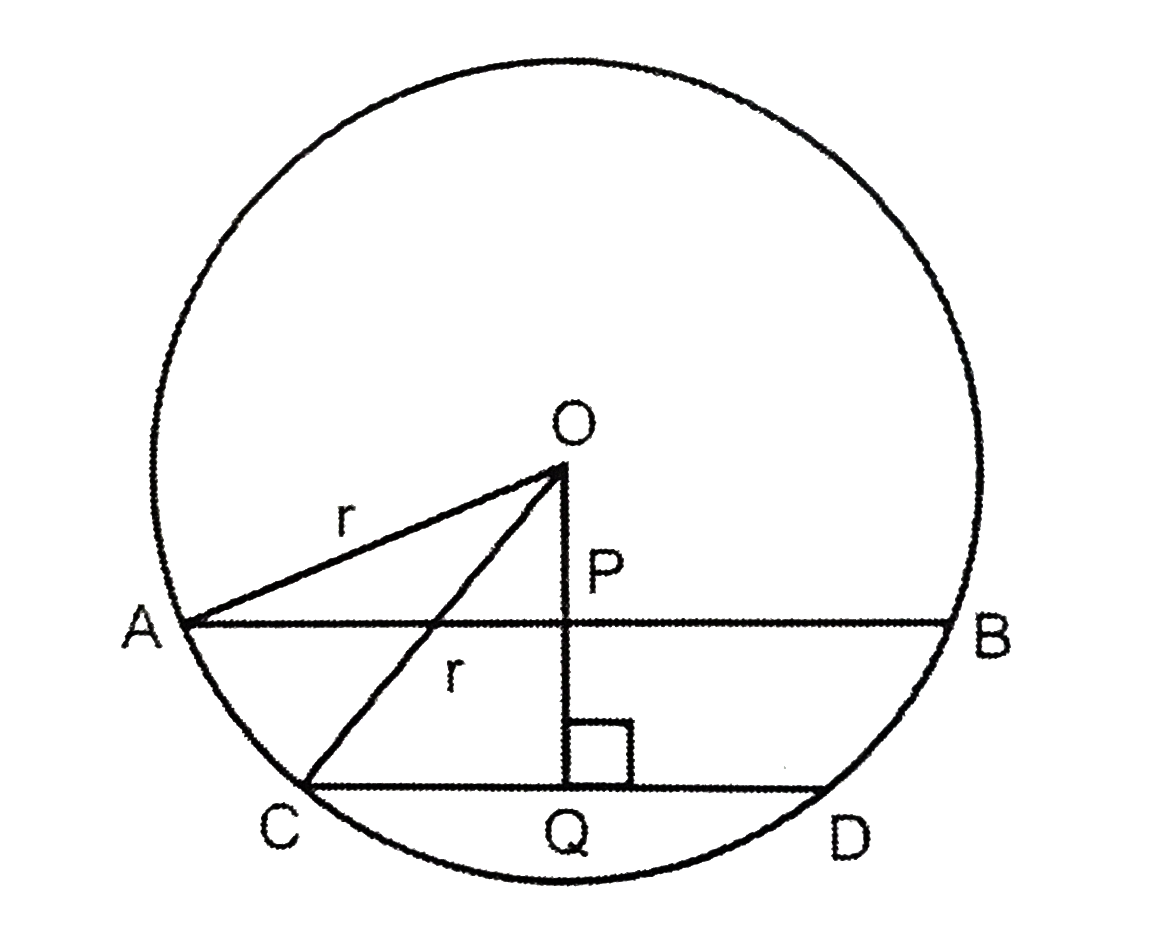
2 parallel chords 24 cm, and 18 cm, are on the same side of the centre of a circle. If the distance between the chords is 3 cm, calculate the radius of the circle.A15 cmB14 cmC13 cmD12 cm
The perpendicular from the centre of a circle to a chord bisects the chord.
View SolutionProve that the line joining the mid-point of a chord to the centre of the circle passes through the mid-point of the corresponding minor arc.
View SolutionIf two equal chords of a circle in intersect within the circle, prove that : the segments of the chord are equal to the corresponding segments of the other chord. the line joining the point of intersection to the centre makes equal angles with the chords.
View SolutionIf two equal chords of a circle in intersect within the circle, prove that: the segments of the chord are equal to the corresponding segments of the other chord. the line joining the point of intersection to the centre makes equal angles with the chords.
View SolutionDescribe :
The locus of the mid-points of all chords parallel to a given chord of a circle.
View SolutionFind the locus of the centre of the circle passing through the vertex and the mid-points of perpendicular chords from the vertex of the parabola y2=4ax .
View SolutionProve that the line joining the mid-points of two parallel chords of a circle passes through the centre.
View Solution