The point of inflection of the curve y=(x−1)3 is Solution in Tamil
(0,0)
(0,1)
(1,0)
(1,1)
The correct Answer is:A
Step by step video, text & image solution for The point of inflection of the curve y=(x-1)^(3) is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- APPLICATIONS OF DIFFERENTIAL CALCULUS BOOK - FULL MARKSCHAPTER - APPLICATIONS OF DIFFERENTIAL CALCULUS EXERCISE - ADDITIONAL QUESTIONS SOLVED
56 Videos
- APPLICATIONS OF DIFFERENTIAL CALCULUS BOOK - FULL MARKSCHAPTER - APPLICATIONS OF DIFFERENTIAL CALCULUS EXERCISE - EXERCISE - 7.9
2 Videos
- APPLICATIONS OF INTEGRATIONBOOK - FULL MARKSCHAPTER - APPLICATIONS OF INTEGRATIONEXERCISE - ADDITIONAL PROBLEMS
35 Videos
Similar Questions
A water tank has the shape of an invertd circular cone with base radius 2 metres and height 4 metres. If water is being pumped into the tank at the rate of 2m3/mm. Find the rate at which the water level is rising when the water is 3m deep
View SolutionFind the asymptotes of the following curves:
f(x)=x2x+1
View SolutionEvaluate as the limit of sums : ∫31(2x2+5) dx
View SolutionNumber of points of inflection of curve y=(x-2)^(6)(x-3)^(5) is
View SolutionIf the point (1,3) serves as the point of inflection of the curve y=ax^(3)+bx^(2) then the value of 'a' and 'b' are -
View SolutionConcavity and convexity :
if f''(x)>0∀x∈(a,b) then the curve y=f(x) is concave up ( or convex down) in (a,b) and iff''(x)<0∀x∈(a,b) then the curve y=f(x) is concave down (or convex up ) in (a,b)

Inflection point :
The point where concavity of the curve changes is known as point of inflection (at inflection point f''(x) is equal to 0 or undefined)
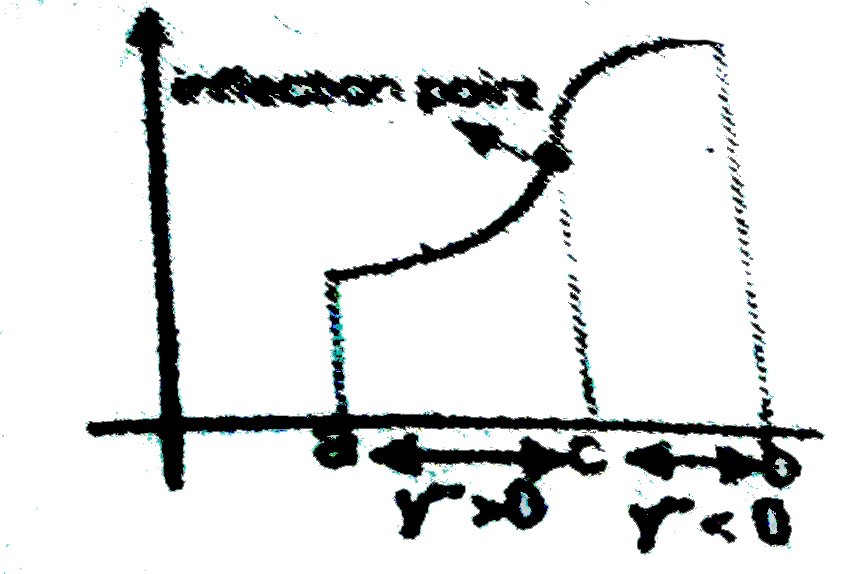
Number of point of inflection for f(x)=(x−1)3(x−2)2 is :
View SolutionConcavity Of Curve And Point Of Inflection
View SolutionFind the coordinates of the point of inflection of the curve f(x) =e^(-x^(2))
View SolutionThe point of inflection of the curve y=(x−1)3 is
View SolutionFind the inflection points of the curve y=(x−5)5/3+2 .
View SolutionDetermine the intervals of concavity of the curve f(x)=(x−2)3(x−4),x∈R and the points of inflection if any.
View SolutionThe point of inflection of the curve y=x4 is at:
View SolutionFind the points of inflection of y=x4−6x2+8x−1
View SolutionA point of inflection of the curve y=e−x2 is
View SolutionDetermine the intervals of concavity of the curve f(x)=(x−1)3(x−5),x∈R and , points of inflection if any
View SolutionIf x0 is the x - coordinate of the point of inflection of a curve y=f(x) then (second derivative exists) ………….. .
View Solution
