The point of inflection of y=x3−5x2+3x−5 is
12
34
74
53
The correct Answer is:D
To find the point of inflection of the function y=x3−5x2+3x−5, we need to follow these steps:
Step 1: Find the first derivative y′
The first derivative of y is calculated using the power rule of differentiation.
y′=ddx(x3)−ddx(5x2)+ddx(3x)−ddx(5)
Calculating each term:
- The derivative of x3 is 3x2.
- The derivative of 5x2 is 10x.
- The derivative of 3x is 3.
- The derivative of a constant −5 is 0.
Putting it all together:
y′=3x2−10x+3
Step 2: Find the second derivative y′′
Now, we differentiate y′ to find the second derivative.
y′′=ddx(3x2)−ddx(10x)+ddx(3)
Calculating each term:
- The derivative of 3x2 is 6x.
- The derivative of 10x is 10.
- The derivative of a constant 3 is 0.
Putting it all together:
y′′=6x−10
Step 3: Set the second derivative equal to zero
To find the points of inflection, we set the second derivative equal to zero:
6x−10=0
Step 4: Solve for x
Now, we solve for x:
6x=10x=106=53
Step 5: Find the corresponding y value
Now we substitute x=53 back into the original function y to find the corresponding y value.
y=(53)3−5(53)2+3(53)−5
Calculating each term:
- (53)3=12527
- 5(53)2=5⋅259=1259
- 3(53)=5
- −5=−5
Now substituting these values into the equation:
y=12527−1259+5−5
To combine these fractions, we need a common denominator, which is 27:
y=12527−37527+13527−13527y=125−375+135−13527=−25027
Final Result
The point of inflection is:
(53,−25027)
The first derivative of y is calculated using the power rule of differentiation.
- The derivative of 5x2 is 10x.
- The derivative of 3x is 3.
- The derivative of a constant −5 is 0.
Now, we differentiate y′ to find the second derivative.
- The derivative of 10x is 10.
- The derivative of a constant 3 is 0.
To find the points of inflection, we set the second derivative equal to zero:
Now, we solve for x:
Now we substitute x=53 back into the original function y to find the corresponding y value.
- 5(53)2=5⋅259=1259
- 3(53)=5
- −5=−5
The point of inflection is:
Topper's Solved these Questions
- APPLICATIONS OF DERIVATIVESBOOK - MCGROW HILL PUBLICATIONCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Solved Examples ( LEVEL -1 SINGLE CORRECT ANSWER TYPE QUESTIONS )
60 Videos
- APPLICATIONS OF DERIVATIVESBOOK - MCGROW HILL PUBLICATIONCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Solved Examples ( LEVEL -2 SINGLE CORRECT ANSWER TYPE QUESTIONS )
25 Videos
- APPLICATIONS OF DERIVATIVESBOOK - MCGROW HILL PUBLICATIONCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Question for Previous Year.s B-Architecture Entrance Examination Papers
27 Videos
- AREA BY INTEGRATIONBOOK - MCGROW HILL PUBLICATIONCHAPTER - AREA BY INTEGRATIONEXERCISE - Question from Previous Years. B-Architecture Entrance Examination Papers
12 Videos
Similar Questions
Knowledge Check
The slope of the tangent at the point of inflection of y=x3−3x2+6x+2009 is equal to :
A2B3C1D4Concavity and convexity :
if f''(x)>0∀x∈(a,b) then the curve y=f(x) is concave up ( or convex down) in (a,b) and iff''(x)<0∀x∈(a,b) then the curve y=f(x) is concave down (or convex up ) in (a,b)

Inflection point :
The point where concavity of the curve changes is known as point of inflection (at inflection point f''(x) is equal to 0 or undefined)
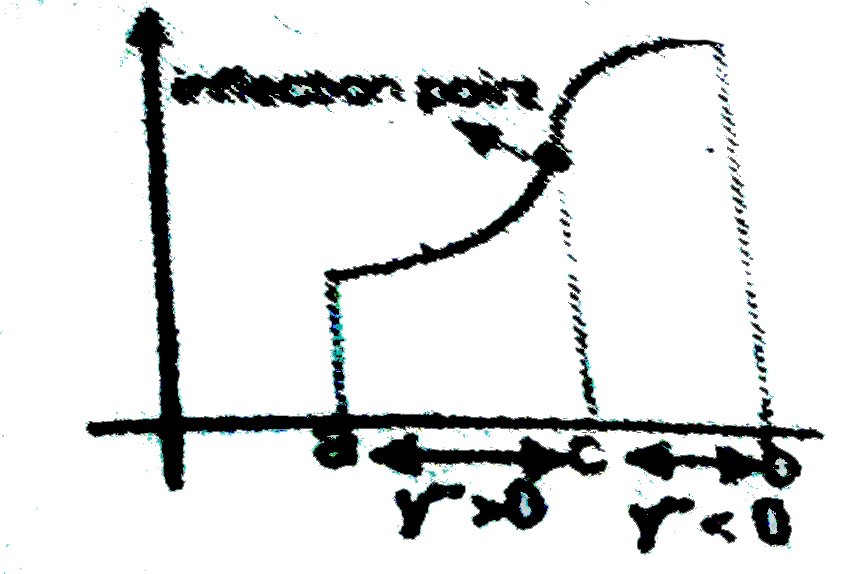
Number of point of inflection for f(x)=(x−1)3(x−2)2 is :A1B2C3D4
Find the points of local maxima, local minima and the points of inflection of the function f(x)=x5−5x4+5x3−1 . Also, find the corresponding local maximum and local minimum values
View SolutionFind the points of inflection for f(x)=sinx f(x)=3x4−4x3
View SolutionNumber of points of inflection for f(x)=x2e−|x| is 1 (b) 2 (c) 3 (d) 4
View SolutionThe point of intersection of X-axis and 3x + 2y - 5 = 0 is _______
View SolutionFind the intervals in which the graphs of the following functions are concave or convex and locate the points of inflection :
y=2−∣∣x5−1∣∣
View SolutionFind the intervals in which the graphs of the following functions are concave or convex and locate the points of inflection :
y=x+x2/3
View Solution