Number of points of inflection for f(x)=x2e−|x| is 1 (b) 2 (c) 3 (d) 4
Step by step video & image solution for Number of points of inflection for f(x)=x^2e^(-|x|) is 1 (b) 2 (c) 3 (d) 4 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
Concavity and convexity :
if f''(x)>0∀x∈(a,b) then the curve y=f(x) is concave up ( or convex down) in (a,b) and iff''(x)<0∀x∈(a,b) then the curve y=f(x) is concave down (or convex up ) in (a,b)

Inflection point :
The point where concavity of the curve changes is known as point of inflection (at inflection point f''(x) is equal to 0 or undefined)
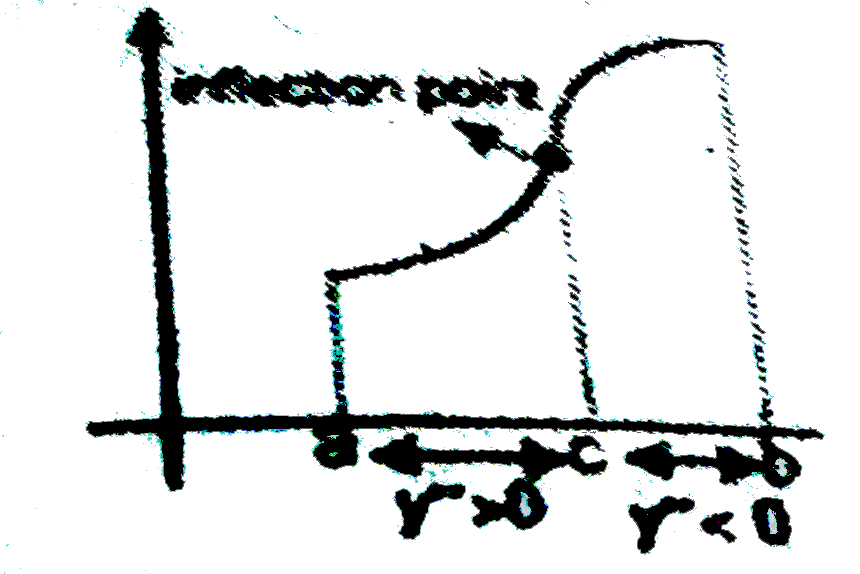
Number of point of inflection for f(x)=(x−1)3(x−2)2 is :A1B2C3D4
If f(x)=1x−1 and g(x)=x−2x+3, then number of points of discontinuity in f(g(x)) is(1)1(2) 2(3) 3(4) 4
View SolutionLet f:(−1,1)→R be defined as f(x)=max(−|x|,−√1−x2), then number of points where it is non-differentiable are equal to (a) 1 (b) 2 (c) 3 (d) 4
View SolutionFind the coordinates of the point of inflection of the curve f(x) =e^(-x^(2))
View Solution[ The number of real solutions of x^(2)-4|x|-2=0 is [ (a) 1, (b) 2 (c) 3, (d) 4]]
View SolutionParagraph for Question Nos. 12 to 14 Consider f(x)=x3⋅(x−2)2⋅(x−1), then 12. The number of distinct real roots of equation f(x)=f(32) is (A) 2 (B) 3 (C)4 (D) 6 13. The number of distinct real roots of equation f(x)=f(23) (D)4 (C)3 (B) 2 (A) 1
View SolutionNumber of points where the function f(x)=(x2−1)∣∣x2−x−2∣∣+sin(|x|) is not differentiable, is: (A) 0 (B) 1 (C) 2 (D) 3
View SolutionThe number of real solutions of the equation ex+(a2+4a+5)x2+6=0 is
(A) 1
(B) 2
(C) 3
(D) 0
View Solution
