The probability that a bulb produced by a factory will fuse after 160 days of use is 0.06. Find the probability that out of 5 such bulbs at the most one bulb will fuse after 160 days of use.
The correct Answer is:3125(4750)4.
To solve the problem, we need to find the probability that at most one bulb will fuse out of five bulbs, given that the probability of a bulb fusing after 160 days is 0.06.
1. Define the probabilities:
- Let p=0.06 (the probability that a bulb will fuse).
- Let q=1−p=1−0.06=0.94 (the probability that a bulb will not fuse).
2. Identify the scenario:
- We are looking for the probability that at most one bulb fuses out of five. This can be expressed as:
P(X≤1)=P(X=0)+P(X=1)
- Here, X is the random variable representing the number of bulbs that fuse.
3. Use the binomial probability formula:
- The probability of exactly r successes (bulbs fusing) in n trials (bulbs) is given by:
P(X=r)=(nr)prqn−r
- In our case, n=5, p=0.06, and q=0.94.
4. Calculate P(X=0):
- For r=0:
P(X=0)=(50)(0.06)0(0.94)5=1⋅1⋅(0.94)5
- Calculate (0.94)5:
(0.94)5≈0.7351
- Thus, P(X=0)≈0.7351.
5. Calculate P(X=1):
- For r=1:
P(X=1)=(51)(0.06)1(0.94)4=5⋅(0.06)⋅(0.94)4
- Calculate (0.94)4:
(0.94)4≈0.7820
- Thus,
P(X=1)=5⋅0.06⋅0.7820≈5⋅0.04692≈0.2346
6. Combine the probabilities:
- Now, we can find P(X≤1):
P(X≤1)=P(X=0)+P(X=1)≈0.7351+0.2346≈0.9697
Final Answer:
The probability that at most one bulb will fuse after 160 days of use is approximately 0.9697.
- Let p=0.06 (the probability that a bulb will fuse).
- Let q=1−p=1−0.06=0.94 (the probability that a bulb will not fuse).
- We are looking for the probability that at most one bulb fuses out of five. This can be expressed as:
P(X≤1)=P(X=0)+P(X=1)
- Here, X is the random variable representing the number of bulbs that fuse.
- The probability of exactly r successes (bulbs fusing) in n trials (bulbs) is given by:
P(X=r)=(nr)prqn−r
- In our case, n=5, p=0.06, and q=0.94.
- For r=0:
P(X=0)=(50)(0.06)0(0.94)5=1⋅1⋅(0.94)5
- Calculate (0.94)5:
(0.94)5≈0.7351
- Thus, P(X=0)≈0.7351.
- For r=1:
P(X=1)=(51)(0.06)1(0.94)4=5⋅(0.06)⋅(0.94)4
- Calculate (0.94)4:
(0.94)4≈0.7820
- Thus,
P(X=1)=5⋅0.06⋅0.7820≈5⋅0.04692≈0.2346
- Now, we can find P(X≤1):
P(X≤1)=P(X=0)+P(X=1)≈0.7351+0.2346≈0.9697
The probability that at most one bulb will fuse after 160 days of use is approximately 0.9697.
Topper's Solved these Questions
- PROBABILITYBOOK - MODERN PUBLICATIONCHAPTER - PROBABILITYEXERCISE - EXERCISE 13 (h) (LATQ)
20 Videos
- PROBABILITYBOOK - MODERN PUBLICATIONCHAPTER - PROBABILITYEXERCISE - Objective Type Question (A. Multiple Choice Questions)
50 Videos
- PROBABILITYBOOK - MODERN PUBLICATIONCHAPTER - PROBABILITYEXERCISE - EXERCISE 13 (g) (SATQ)
2 Videos
- MATRICESBOOK - MODERN PUBLICATIONCHAPTER - MATRICESEXERCISE - CHAPTER TEST (3)
12 Videos
- RELATIONS AND FUNCTIONSBOOK - MODERN PUBLICATIONCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - CHAPTER TEST (1)
12 Videos
Similar Questions
The probability that a bulb produced by a factory will fuse after 150 days if used is 0.05. what is the probability that out of 5 such bulbs none will fuse after 150 days of use? 1−(1920)5 b. (1920)5 c. (34)5 d. 90(14)5
View SolutionThe probability that a bulb produced by a factory will fuse after 6 months of use is 0.05 . Find the probability that out of 5 such bulbs
(i) none will fuse after 6 months of use
(ii) at least one will fuse after 6 months of use
(iii) not more than one will fuse after 6 months of use.
View Solution
Knowledge Check
The probability that a bulb produced by a factory will fuse after 150 days of use is 0.05. What is the probability that out of 5 such bulbs none will fuse after 150 days of use?
A1−(1920)5B(1920)5C(34)5D90(14)5The probability that tulb produced by a factor will fuse after 150 days if used is 0.50. What is the probability that out of 5 such balbs none will fuse after 150 days of use ?
A1−(19/20)5B(19/20)5C(3/4)5D90(1/4)5
The probability that a bulb produced by a factory will fuse after 150 days of use is 0.05. Find the probability that out of 5 such bulbs(i) none(ii) not more than one(iii) more than one(iv) at least onewill fuse after 150 days of use.
View SolutionThe probability that a bulb produced by a factory will fuse after an year of use is 0.1. Then the probability that out of 4 such bulbs, only one is working after an year
View SolutionThe probability that a bulb produced by a factory will fuse after 150 days of use is 0.05. Find the probability that out of 5 such bulbs :
(i) none
(ii) none more than one
(iii) more than one
(iv) at least one
will fuse after 150 days of use.
View SolutionThe probability that a bulb produced by a factory will fuse after 200 days of use is 0.2. Let X denote the number of bulbs (out of 5 ) that fuse after 200 days of use . Find the probability of
(i)X=0,(ii)X≤1,(iii)X>1,(iv)X≥1.
View SolutionThe probability that a bulb produced by a factory will fuse after 150 days of use is 0.05. If a sample of such 5 bulbs are taken out, then match the probabilities in column I with their respective values in column II and choose the correct option from the codes given below.
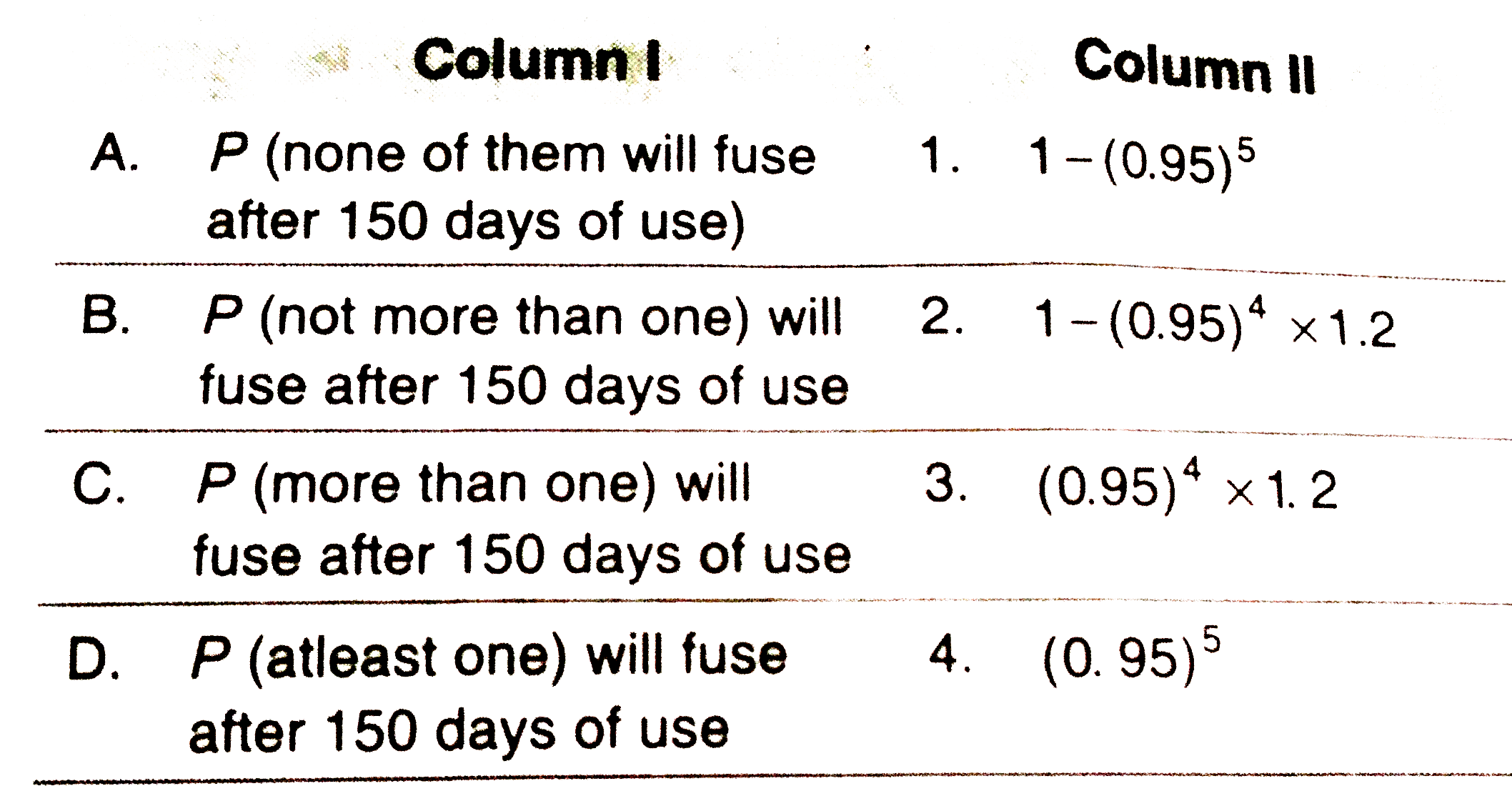
View SolutionThe probability that the life of a bulb is 100 days is 0.05. Find the probability that out of 6 bulbs (i) atleast 1 (ii) greater than 4 (iii) none will be having a life of 100 days
View Solution
