The random variable 'X' has a probability distribution P (X) of the following form, where k is some number :
P(X)=⎧⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪⎩k,ifX=02k,ifX=13k,ifX=20,ifotherwise
(a) Determine the value of k.
(b) Find P(X<2),P(X≤2),P(X≥2)
The correct Answer is:(a) k=16 (b) (i) 0.5 (ii) 1 (iii) 0.5
To solve the given problem, we need to determine the value of k in the probability distribution and then calculate the required probabilities. Let's break it down step by step.
Step 1: Determine the value of k
The probability distribution P(X) is defined as follows:
- P(X=0)=k
- P(X=1)=2k
- P(X=2)=3k
- P(X otherwise)=0
Since the sum of all probabilities must equal 1, we can write the equation:
P(X=0)+P(X=1)+P(X=2)=1
Substituting the values we have:
k+2k+3k=1
Combining like terms gives:
6k=1
Now, solving for k:
k=16
Step 2: Find the probabilities
Now that we have k, we can substitute it back into the probability distribution:
- P(X=0)=k=16
- P(X=1)=2k=26=13
- P(X=2)=3k=36=12
Step 3: Calculate P(X<2)
To find P(X<2), we need to consider the values of X that are less than 2, which are X=0 and X=1:
P(X<2)=P(X=0)+P(X=1)=16+13
To add these fractions, we need a common denominator. The least common multiple of 6 and 3 is 6:
P(X<2)=16+26=36=12
Step 4: Calculate P(X≤2)
To find P(X≤2), we include X=0,1, and 2:
P(X≤2)=P(X=0)+P(X=1)+P(X=2)=16+13+12
Again, we need a common denominator, which is 6:
P(X≤2)=16+26+36=66=1
Step 5: Calculate P(X≥2)
To find P(X≥2), we consider X=2 and values greater than 2 (which have a probability of 0):
P(X≥2)=P(X=2)+P(X>2)=P(X=2)+0=12
Summary of Results
(a) The value of k is 16.
(b) The probabilities are:
- P(X<2)=12
- P(X≤2)=1
- P(X≥2)=12
- P(X=1)=2k
- P(X=2)=3k
- P(X otherwise)=0
- P(X=1)=2k=26=13
- P(X=2)=3k=36=12
- P(X<2)=12
- P(X≤2)=1
- P(X≥2)=12
Topper's Solved these Questions
- PROBABILITYBOOK - MODERN PUBLICATIONCHAPTER - PROBABILITYEXERCISE - MOCK TEST (Select the correct option)
10 Videos
- PROBABILITYBOOK - MODERN PUBLICATIONCHAPTER - PROBABILITYEXERCISE - MOCK TEST (Fill in the blanks)
7 Videos
- PROBABILITYBOOK - MODERN PUBLICATIONCHAPTER - PROBABILITYEXERCISE - COMPETITION FILE
17 Videos
- MATRICESBOOK - MODERN PUBLICATIONCHAPTER - MATRICESEXERCISE - CHAPTER TEST (3)
12 Videos
- RELATIONS AND FUNCTIONSBOOK - MODERN PUBLICATIONCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - CHAPTER TEST (1)
12 Videos
Similar Questions
The random variable X has a probability distribution P(X) of the following form, where k is some number :P(X) = {(k,ifx=0),(2k,ifx=1),(3k,ifx=2),(0otherwise)(a) Determine k.(b) Find P (X<2) , P (X≤2) , P(X≥2)
View SolutionA random variable 'X' has a probability distribution P(X) of the following form (k is constant):

then k = __________ .
View Solution
Knowledge Check
Let denote the number of fruits that are grown in a farm house in a particular day. The probability that X can take the value of x has the following form, where k is some unknown constant.
P(X=x)=⎧⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪⎩kifx=02kifx=13xifx=20otherwise
Then the value of k isA18B12C13D16
Let 'X' denote the number of hours you study during a randomly selected school day. The probability that 'X' can take the values of x has the following form, where k is some unknown constant.
P(X=x)={(0.1,,if,x=0),(kx,,if,x=1 or 2),(k(5−x),,if,x=3 or 4),(0,,,otherwise.
(a) Find the value of 'k'.
(b) What is the probability that you study at least two hours ? Exactly two hours ? At most two hours ?
View SolutionA random variable X has the following probability distribution:
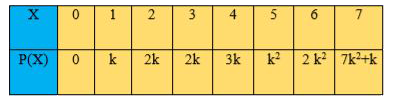
Determine : (i) k (ii) P(X<3) (iii) P(X>4)
View SolutionThe probability distribution of X is as follows:
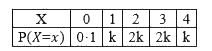
Find k and P [X<2].
View SolutionA random variable 'X' has the following probability distribution :

Find : (i) the value of K (ii) P(X≤1)
(iii) P(X≥0).
View SolutionA random variable X has the following probability distribution:Determine (i) k (ii) P(X<3)(iii) P(X>6) (iv) P(0<X<3)
View SolutionA random variable X has the following probability distribution: X=xi: 1 2 3 4 P(X=xi): k 2k 3k 4k Write the value of P(X≥3) .
View SolutionFind k,P(X<1),P(0<x<3).
View Solution
