The ratio in which the line x−1=0 divides the area bounded by the curves 2x+1=√4y+1,y=xandy=2 isSolution in Tamil
We have 2x+1=√4y+1 ...(1)
or (2x+1)2=4y+1
or y=x2+x ...(2)
∴ Curve (1) is part of the parabola (2), for x≥−1/2.
Differentiating (2), w.r.t. x, we get
dydx=2x+1
∴ (dydx)x=0=1.
∴ line y=x is tangent to curve (2) at (0,0).
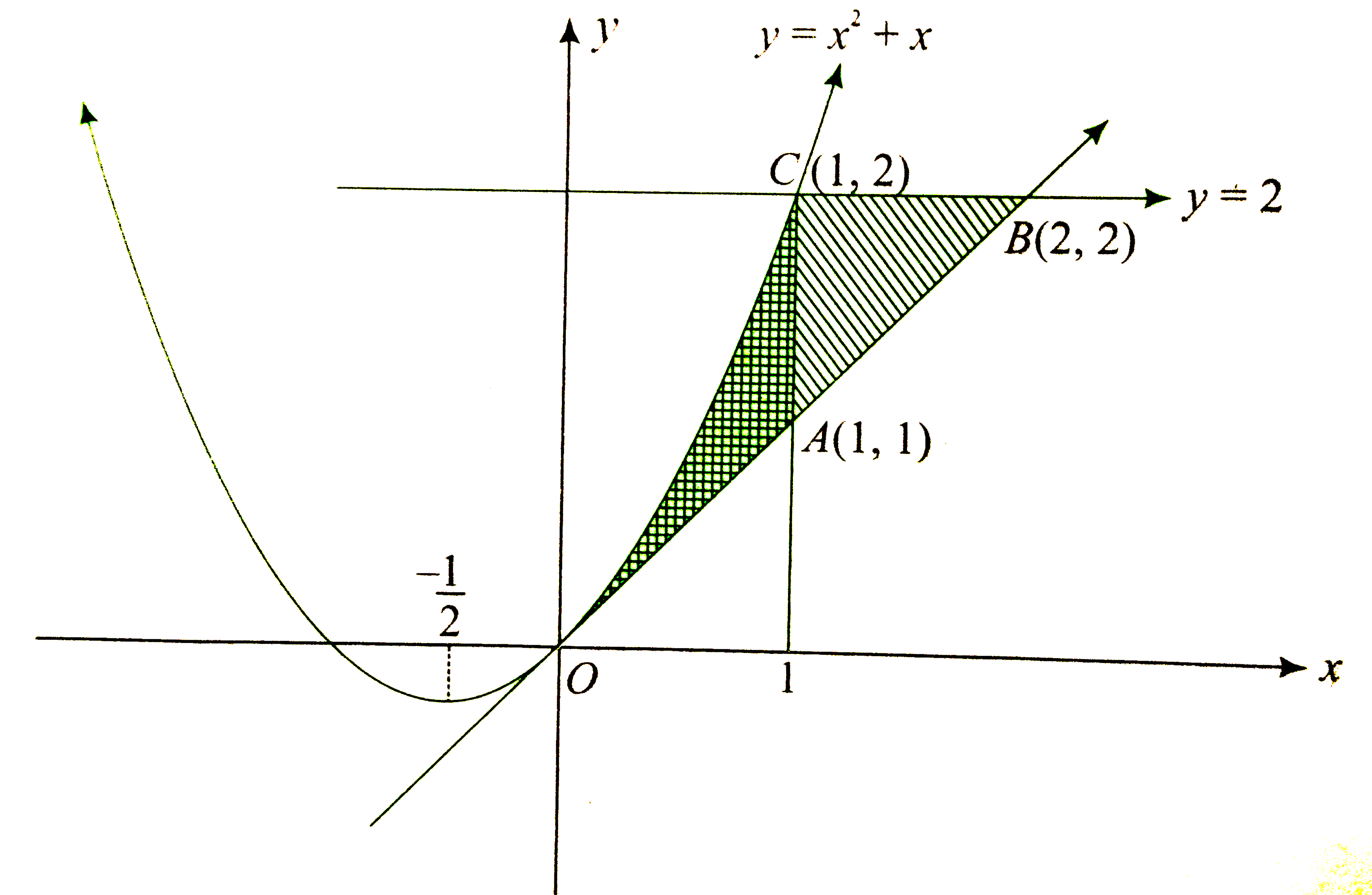
From the figure,
Area of the region OACOis=1∫0(x2+x−x)dx
=[x33]10=13
Area of the triangle ACBis=12×1×1=12
∴ Required ratio =1/31/2=23
Topper's Solved these Questions
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.1
9 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.2
14 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type
2 Videos
- AREA UNDER CURVESBOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank
10 Videos
Similar Questions
Find the area of the smaller part of the circle x2+y2=a2 cut off by the line x=a√2.
View SolutionFind the area lying in the first quadrant and bounded by the curve y=x3 and the line y=4x.
View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
View SolutionThe area of the region (s) enclosed by the curves y=x2 and y=√|x| is
View SolutionIf the line x-1=0 divides the area bounded by the curves 2x+1=sqrt(4y+1),y=x and y=2 in two regions of area A_(1) and A_(2)(A_(1)
View SolutionFind the area bounded by the curves y=sqrt(1-x^(2)) and y=x^(3)-x .Also find the ratio in which they-axis divided this area.
View SolutionThe ratio in which the area bounded by the curves y2=xandx2=y is divided by the line x=12 is
View SolutionFind the ratio in which y=sqrt(5-x^(2)) divides the area of the region bounded by x^(2)-4y=0 and 2x-y=0
View SolutionFind the area of the region bounded by the curves y=√x+2andy=1x+1 between the lines x=0 and x=2.
View SolutionThe ratio in which the line x−1=0 divides the area bounded by the curves 2x+1=√4y+1,y=xandy=2 is
View SolutionThe area bounded by the curve y2=1−x and the lines y=[x]x,x=−1,andx=12 is
View SolutionThe area of the region bounded by the curves 2x=y2−1 and x=0
View SolutionFind the area bounded by the curve y = (2x)/(1 + x^(2)) and the lines x = -1 ,x = 2 and the x-axis
View SolutionThe area of the region bounded by curves y=1−x2,x+y+1=0andx−y−1=0 is
View SolutionFind the area of the region bounded by the curves y=√x+2andy=1x+1 between the lines x=0 and x=2.
View Solution
