The area bounded by the curve y2=1−x and the lines y=[x]x,x=−1,andx=12 is
A
3√2−116 sq. units
B
3√2−114 sq. units
C
6√2−115 sq. units
D
None of these
Video Solution
Text Solution
The correct Answer is:A
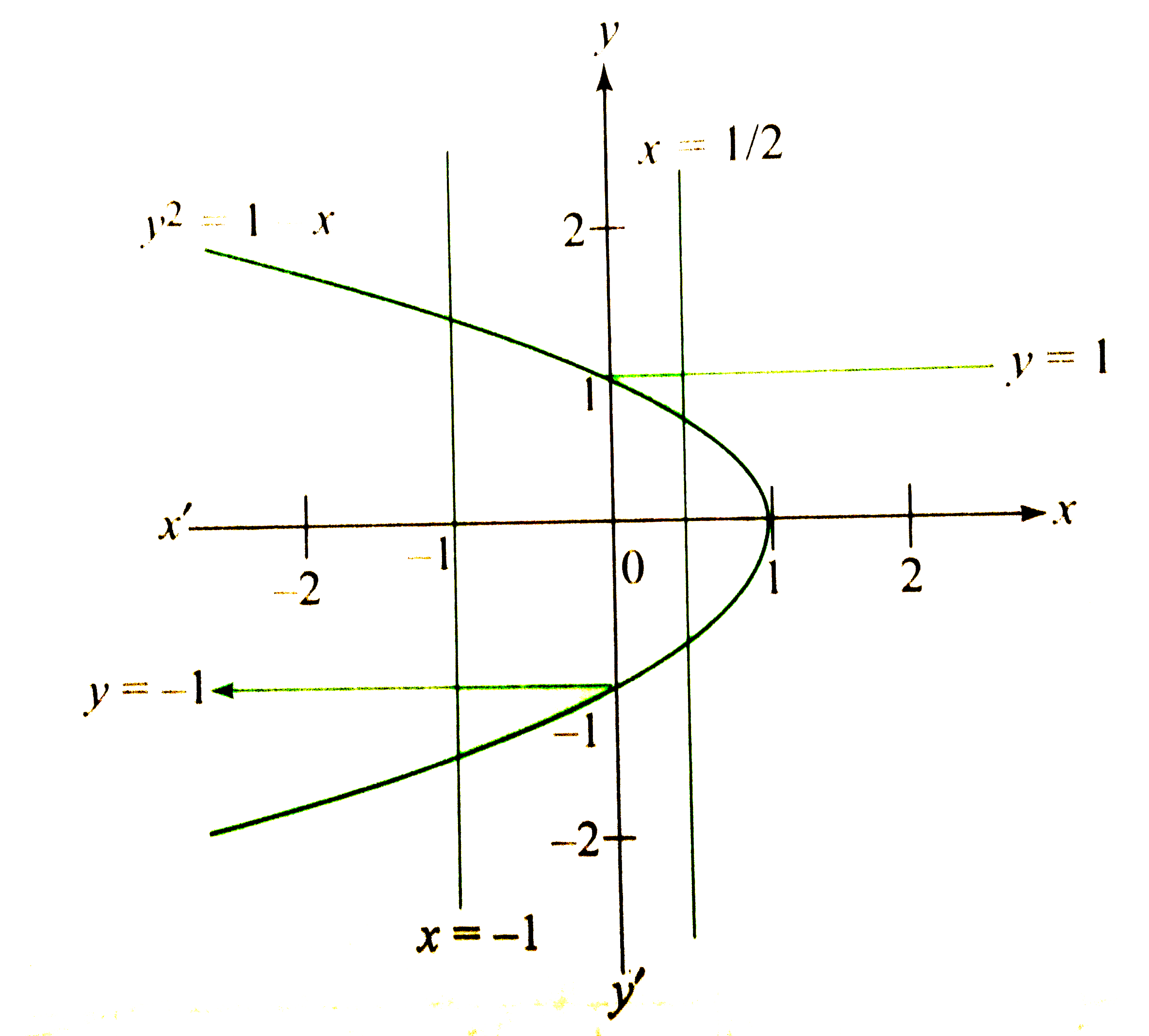
From the figure,
A=0∫−1(−1−(−√1−x))dx+1/2∫0(1−√1−x)dx
=[−x−(1−x)3/23/2]0−1+[x+(1−x)3/23/2]1/20
=[−23−(1−2×23/23)]+[12+23×23/2−23]
=3√3−43−12
=3√2−116 sq. units
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Multiple)10videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Comprehension)21videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.37videos
AREA
- BOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Question Bank29videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank20videos
AREA UNDER CURVES
Similar Questions
Knowledge Check
- Question 1 - Select One
The area bounded by the curve y2=8x and the line x=2 is
A323 sq. unitsB233 sq. unitsC163 sq. unitsD132 sq. units - Question 2 - Select One
The area bounded by the curve y=x(x2−1) and x-axis is
A0B12C1D14 - Question 3 - Select One
The area bounded by the curve y=x2, X-axis and the lines x = 1, x = 3 is
A263sq.unitsB283sq.unitsC13sq.unitsD9 sq. units
The area bounded by the curves y=xex,y=xe−x and the lines x=1 is
View SolutionThe area bounded by the curve y=|x|−1andy=−|x|+1 is
View SolutionThe area bounded by the curves y=|x|−1andy=−|x|+1 is 1 b. 2 c. 2√2 d. 4
View SolutionArea bounded by the curves y=x2−1,x+y=3 is
View SolutionThe area bounded by the curve y2=14x and the lines x = 1, x = 4 above X-axis is
View Solution

