The table below shows the daily expenditure on food of 25 households in a locality. daily expenditure(in rs) 100-150 150-200 200-250 250-300 300-350 no. of households 4 5 12 2 2 Find the mean daily expenditure on food by a suitable method.
To find the mean daily expenditure on food based on the given data, we will follow these steps:
Step 1: Create a Frequency Table
We will create a frequency table that includes the class intervals (daily expenditure), the number of households (frequency), and the midpoints of each class interval.
| Daily Expenditure (in Rs) | No. of Households (f) | Midpoint (xi) |
|----------------------------|-----------------------|---------------|
| 100 - 150 | 4 | 125 |
| 150 - 200 | 5 | 175 |
| 200 - 250 | 12 | 225 |
| 250 - 300 | 2 | 275 |
| 300 - 350 | 2 | 325 |
Step 2: Calculate the Midpoints
The midpoint (xi) for each class interval is calculated as follows:
- For 100 - 150: (100 + 150) / 2 = 125
- For 150 - 200: (150 + 200) / 2 = 175
- For 200 - 250: (200 + 250) / 2 = 225
- For 250 - 300: (250 + 300) / 2 = 275
- For 300 - 350: (300 + 350) / 2 = 325
Step 3: Calculate f * xi
Now, we will calculate the product of the frequency (f) and the midpoint (xi) for each class interval.
| Daily Expenditure (in Rs) | No. of Households (f) | Midpoint (xi) | f * xi |
|----------------------------|-----------------------|---------------|--------|
| 100 - 150 | 4 | 125 | 500 |
| 150 - 200 | 5 | 175 | 875 |
| 200 - 250 | 12 | 225 | 2700 |
| 250 - 300 | 2 | 275 | 550 |
| 300 - 350 | 2 | 325 | 650 |
Step 4: Sum of f and Sum of f * xi
Now we will calculate the total of the frequencies and the total of f * xi.
- Sum of f (Σf) = 4 + 5 + 12 + 2 + 2 = 25
- Sum of f * xi (Σf * xi) = 500 + 875 + 2700 + 550 + 650 = 4875
Step 5: Calculate the Mean
We can now calculate the mean using the formula:
Mean=Σf⋅xiΣf
Substituting the values we calculated:
Mean=487525=195
Final Answer
The mean daily expenditure on food is Rs. 195.
---
We will create a frequency table that includes the class intervals (daily expenditure), the number of households (frequency), and the midpoints of each class interval.
|----------------------------|-----------------------|---------------|
| 100 - 150 | 4 | 125 |
| 150 - 200 | 5 | 175 |
| 200 - 250 | 12 | 225 |
| 250 - 300 | 2 | 275 |
| 300 - 350 | 2 | 325 |
The midpoint (xi) for each class interval is calculated as follows:
- For 100 - 150: (100 + 150) / 2 = 125
- For 150 - 200: (150 + 200) / 2 = 175
- For 200 - 250: (200 + 250) / 2 = 225
- For 250 - 300: (250 + 300) / 2 = 275
- For 300 - 350: (300 + 350) / 2 = 325
Now, we will calculate the product of the frequency (f) and the midpoint (xi) for each class interval.
|----------------------------|-----------------------|---------------|--------|
| 100 - 150 | 4 | 125 | 500 |
| 150 - 200 | 5 | 175 | 875 |
| 200 - 250 | 12 | 225 | 2700 |
| 250 - 300 | 2 | 275 | 550 |
| 300 - 350 | 2 | 325 | 650 |
Now we will calculate the total of the frequencies and the total of f * xi.
- Sum of f * xi (Σf * xi) = 500 + 875 + 2700 + 550 + 650 = 4875
We can now calculate the mean using the formula:
The mean daily expenditure on food is Rs. 195.
Topper's Solved these Questions
Similar Questions
The table below shows the daily expenditure on food of 30 households in a locality:
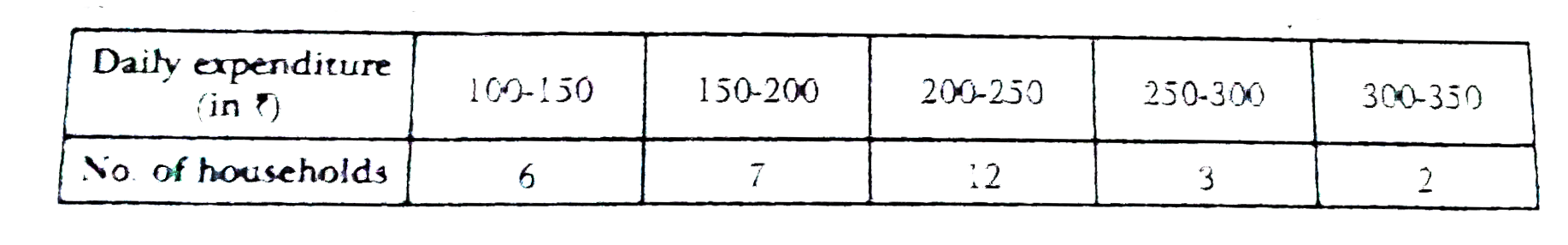
Find the mean daily expenditure on food.View SolutionThe table below shows the daily expenditure on food of 25 households in a locality.Find the mean daily expenditure on food by a suitable method.
View SolutionThe following table gives the distribution of total household expenditure (in rupees) of manual workers in a city. Expenditure: (in Rs.) 100-150 150-200 200-250 250-300 300-350 350-400 400-450 450-500 Frequency: 24 40 33 28 30 22 16 7 Find the average expenditure (in Rs.) per household.
View SolutionThe following table gives the distribution of total household expenditure (in rupees) of manual workers in a city. Expenditure (in rupees) (xi) Frequency (fi) 100-150 24 150-200 40 200-250 33 250-300 28 300-350 30 350-450 22 400-450 16 450-500 7 Find the average expenditure (in rupees) per household.
View SolutionThe following table gives the daily income of 50 workers of a factory: Daily income (in Rs): 100-120 120-140 140-160 160-180 180-200 Number of workers: 12 14 8 6 10 Find the mean, mode and median of the above data.
View SolutionFind the median of the following data: Classes: 0-50 50-100 100-150 150-200 200-250 250-300 300-350 Frequency: 2 3 5 6 5 3 1
View SolutionThe monthly profits (in Rs.) of 100 shops are distributed as follows: Profits per shop: 0-50 50-100 100-150 150-200 200-250 250-300 No. of shops: 12 18 27 20 17 6 Draw the frequency polygon for it.
View SolutionConsider the following distribution of daily wages of 50 workers of a factory. Daily wages (in Rs).: 100-120 120-140 140-160 160-180 180-200 Numberof workers: 12 14 8 6 10 Findthe mean daily wages of the workers of the factory by using an appropriate method.
View SolutionThe daily wages (in ₹) of 15 workers in a factory are given below :
195, 185, 145, 155, 135, 180, 175, 200, 150, 125, 190, 180, 170, 175, 190
Find the mean daily wage.View SolutionThe following data gives the distribution of total monthly household expenditure of 200 families of a village. Find the modal monthly expenditure of the families. Also, find the mean monthly expenditure: Expenditure (Rs.) Frequency Expenditure (Rs.) Frequency 1000-1500 24 3000-3500 30 1500-2000 40 3500-4000 22 2000-2500 33 4000-4500 16 2500-3000 28 4500-5000 7
View Solution

