The tagents at any point P of the circle x2+y2=16 meets the tangents at a fixed point A at T. Point is joined to B, the other end of the diameter, through, A.
Which of the following does not change by changing the radius of the circle ?
Coordinartes of foci
Length of he major axis
Eccentricity
Length of the minor axis
Tangent at P(4cosθ,4sinθ)→x2+y2=16 is xcosθy+sinθ=4 (1)
The equation of AP is y=sinθcosθ−1(x−4) (2)
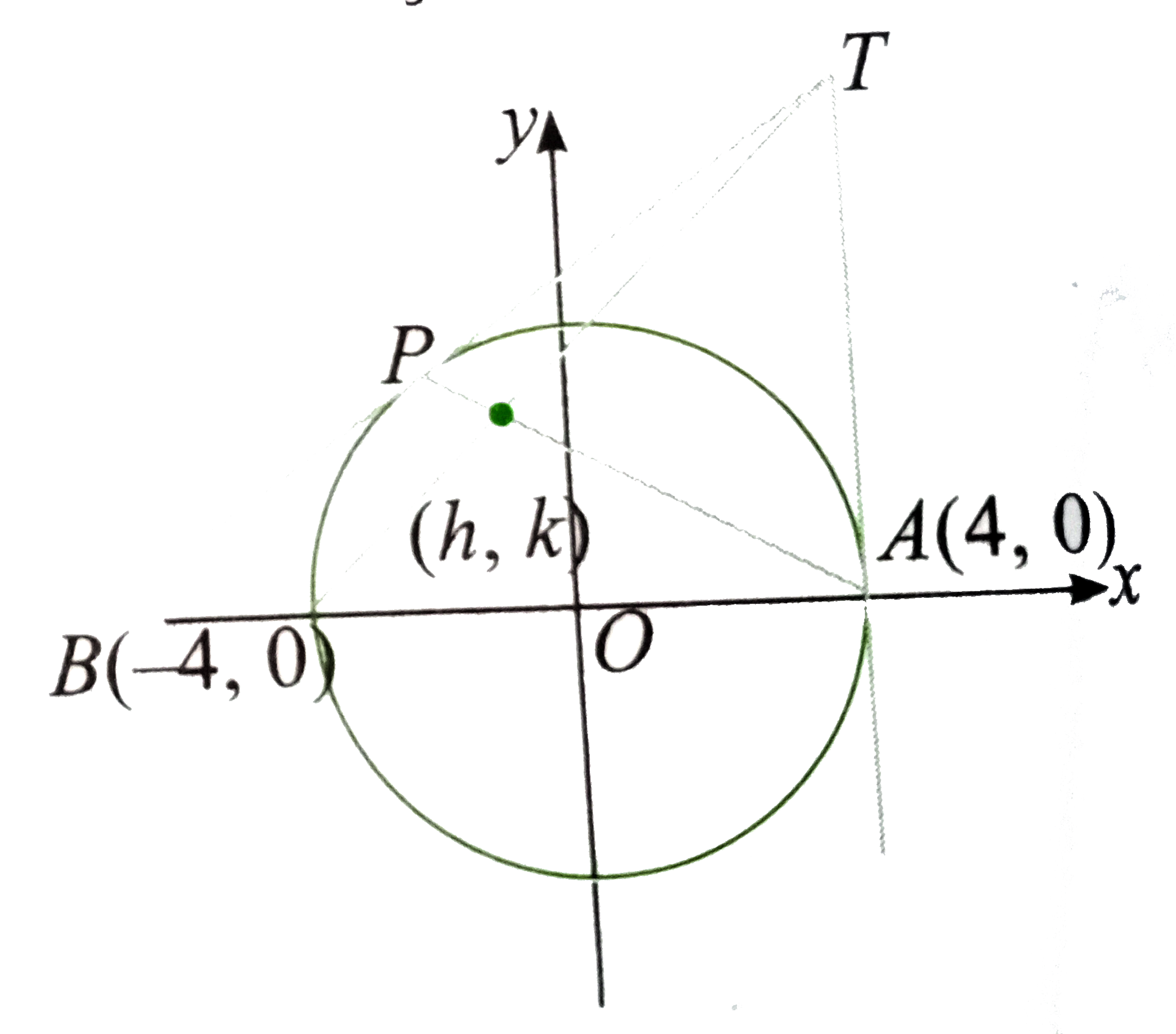
From (1), the coordinates of the point T are given by
(4,4(1−cosθ)sinθ)
The equation of BT is y=1−cosθ2sinθ(x+4) (3)
Let (h,k) be the point of intersection of the lines (2), and (3). Then we have
k2=−12(h2−16)
or h216+y28=1
Therefore, the locus of (h,k) is x216+y28=1
Which is an ellipse with eccehntrically e=1/√2
Sum of focal distance of any points is 2a=8
Considering the circle x2+y2=a2, we find the that the eccentricity of the ellipse is 1√2 which is contant and does not change by changing the radius of the circle
Similar Questions
The tagents at any point P of the circle x2+y2=16 meets the tangents at a fixed point A at T. Point is joined to B, the other end of the diameter, through, A.
The sum of focal distance of any point on the curce is
View SolutionThe tagents at any point P of the circle x2+y2=16 meets the tangents at a fixed point A at T. Point is joined to B, the other end of the diameter, through, A.
The locus of the intersection of AO and BT is a conic whosee eccentricity is
View Solution
Knowledge Check
The tagents at any point P of the circle x2+y2=16 meets the tangents at a fixed point A at T. Point is joined to B, the other end of the diameter, through, A.
The sum of focal distance of any point on the curce isA12B16C20D8The tagents at any point P of the circle x2+y2=16 meets the tangents at a fixed point A at T. Point is joined to B, the other end of the diameter, through, A.
The locus of the intersection of AO and BT is a conic whosee eccentricity isA1/2B1/√2C1/3D1/√3If tangent at any point P on the ellipse 7x2+16y2=12 cuts the tangent at the end points of the major axis at the points A and B, then the circle with AB as diameter passes through a fixed point whose coordinates are
A(±√a2−b2,0)B(±√a2+b2,0)C(0,±√a2−b2)D(0,√a2+b2)
The tangent at any point P of a circle x2+y2=a2 meets the tangent at a fixed point A(a,0) in T and T is joined to B, the other end of the diameter through A, prove that the locus of the intersection of AP and BT is an ellipse whose eccentricity is 1√2
View SolutionThe tangent at any point P on the circle x2+y2=4 meets the coordinate axes at AandB . Then find the locus of the midpoint of AB.
View SolutionThe tangent at any point to the circle x2+y2=r2 meets the coordinate axes at A and B.If the lines drawn parallel to axes through A and B meet at P then locus of P is
View SolutionThe tangent at any point to the circle x2+y2=r2 meets the coordinate axes at A and B. If the lines drawn parallel to axes through A and B meet at P then locus of P is
View SolutionA variable circle passes through the fixed point A(p, q) and touches x-axis. The locus of the other end of the diameter through A is:
View Solution
