The two circles which pass through (0,a)and(0,−a) and touch the line y=mx+c will intersect each other at right angle if a2=c2(2m+1) a2=c2(2+m2) c2=a2(2+m2) (d) c2=a2(2m+1)Solution in Tamil
a2=c2(2m+1)
a2=c2(2+m2)
c2=a2(2+m2)
c2=a2(2m+1)
The correct Answer is:3
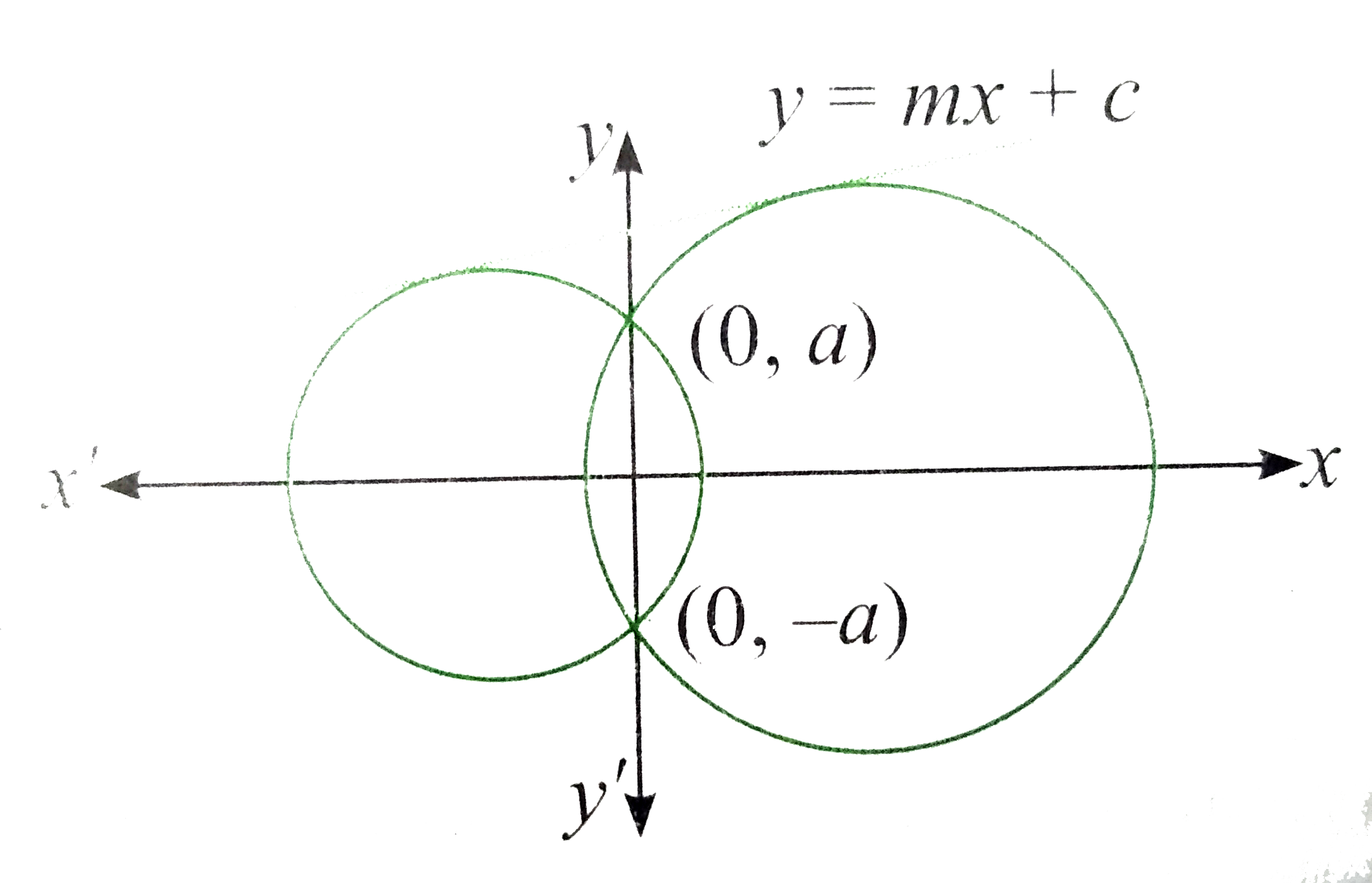
The equatio of the family of circles through (0,a) and (0,-a) is
[x2+(y−a)(y+a)]+λx=0,λ∈R
or x2+y2+λx−a2=0
Since circles touch line y=mx+c,
√(λ2)2+a2=|(−mλ/2)+c|√1+m2
or (1+m2)[λ24+a2]=(mλ2−c)2
or (1+m2)[λ24+a2]=m2λ24−mcλ+c2
or λ2+4mcλ+4a2(1+m2)−4c2=0
∴λ1λ2=4[a(1+m2)−c2]
or g1g2=[a2(1+m2)−c2]
Now, g1g2=f1f2=c1+c22 (As circle cut orthogonally.)
∴a2(1+m2)−c2=−a2
Hence, c2=a2(2+m2)
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Multiple)
25 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Comprehension)
46 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise 4.6
5 Videos
- BINOMIAL THEOREMBOOK - CENGAGECHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
16 Videos
Similar Questions
about to only mathematics
View SolutionEach side of a square is of length 6 units and the centre of the square Is ( - 1, 2). One of its diagonals is parallel to x+y=0. Find the co-ordinates of the vertices of the square.
View SolutionIf the circle x2+y2+2x+3y+1=0 cuts x2+y2+4x+3y+2=0 at AandB , then find the equation of the circle on AB as diameter.
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
View SolutionThe two circles x2+y2=ax and x2+y2=c2(c>0) touch each other if : (1) 2|a|=c (2) |a|=c (3) a=2c (4) |a|=2c
View SolutionThe two circles which pass through (0,a)and(0,−a) and touch the line y=mx+c will intersect each other at right angle if (A) a2=c2(2m+1) (B) a2=c2(2+m2) (C)c2=a2(2+m2) (D) c2=a2(2m+1)
View SolutionFind the value of ∫(xm−1)dxxm+1√1−2xm+mx2m (A) √m+2xm+1x2m+c (B) √m−2xm+1x2m+c (C) √m−2xm−1x2m+c (D) √m+2xm−1x2m+c
View SolutionShow that the circles x^2 +y^2 + 2ax + c = 0 and x^2 + y^2 + 2by + c = 0 touch each other if 1//a^2 + 1//b^2 = 1//c.
View SolutionProve that the circles x2+y2+2ax+c2=0andx2+y2+2by+c2=0 touch each other, if 1a2+1b2=1c2.
View SolutionIf two circles x2+y2−2ax+c==0 and
x2+y2−2by+c=0 touch each other , then c =
View SolutionThe two circles x2+y2=ax,x2+y2=c2(c>0) touch each other if
View Solutionसिद्ध कीजिए कि वृत्त x2+y2+2ax+c=0 और x2+y2+2by+c=0 एक - दूसरे को स्पर्श करेंगे , यदि 1a2+1b2=1c.
View SolutionThe two circles which pass through (0,a)and(0,−a) and touch the line y=mx+c will intersect each other at right angle if (A) a2=c2(2m+1) (B) a2=c2(2+m2) (C)c2=a2(2+m2) (D) c2=a2(2m+1)
View SolutionThe two circles x2+y2=axandx2+y2=c2(c>0) touch each other if (1) a=2c (2) |a|=2c (3) 2|a|=c (4) |a|=c
View SolutionIf the equation (1+m2)x2+2mcx+(c2−a2)=0 has equal roots, prove that c2=a2(1+m2).
View Solution
