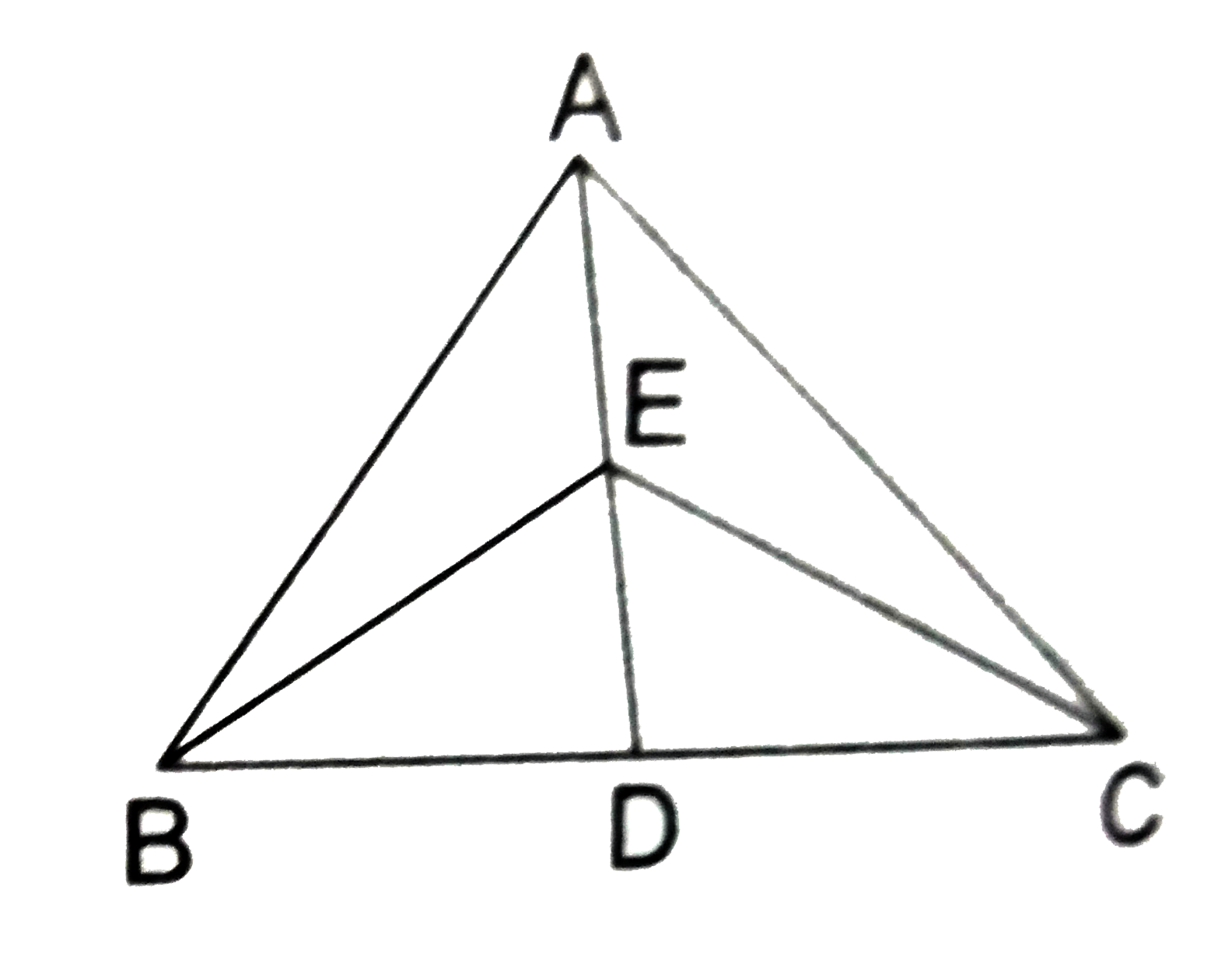
The vertex A of is joined to a point D on BC. IF E is the midpoint of AD then = ?
A
B
C
D
Video Solution
Text Solution
The correct Answer is:A
Median BE in divides it into two of equal area.
.
.
|
Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - ASSERTION & REASON TYPE
5 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - Exercise 11
38 Videos
- AREAS OF TRIANGLES AND QUADRILATERALSBOOK - RS AGGARWALCHAPTER - AREAS OF TRIANGLES AND QUADRILATERALSEXERCISE - Multiple Choice Questions (Mcq)
16 Videos
Similar Questions
Knowledge Check
In △ABC, if D is the midpoint of BC and E is the midpoint of AD then ar(△BED) = ?
 A12ar(△ABC)B13ar(△ABC)C14ar(△ABC)D23ar(△ABC)
A12ar(△ABC)B13ar(△ABC)C14ar(△ABC)D23ar(△ABC)P is any point on the side BC of a △ABC. P is joined to a. If D and E are the midpoints of the sides AB and AC respectively and M and N are the midpoints of BP and CP respectively then quadrilateral DENM is
Aa trapeziumBa parallelogramCa rectangleDa rhombusThe area of ΔABC is 44 cm2 . If D is the midpoint of BC and E is the midpoint of AB, then the area ( in cm2) of ΔBDE is :
A5.5B22C11D44
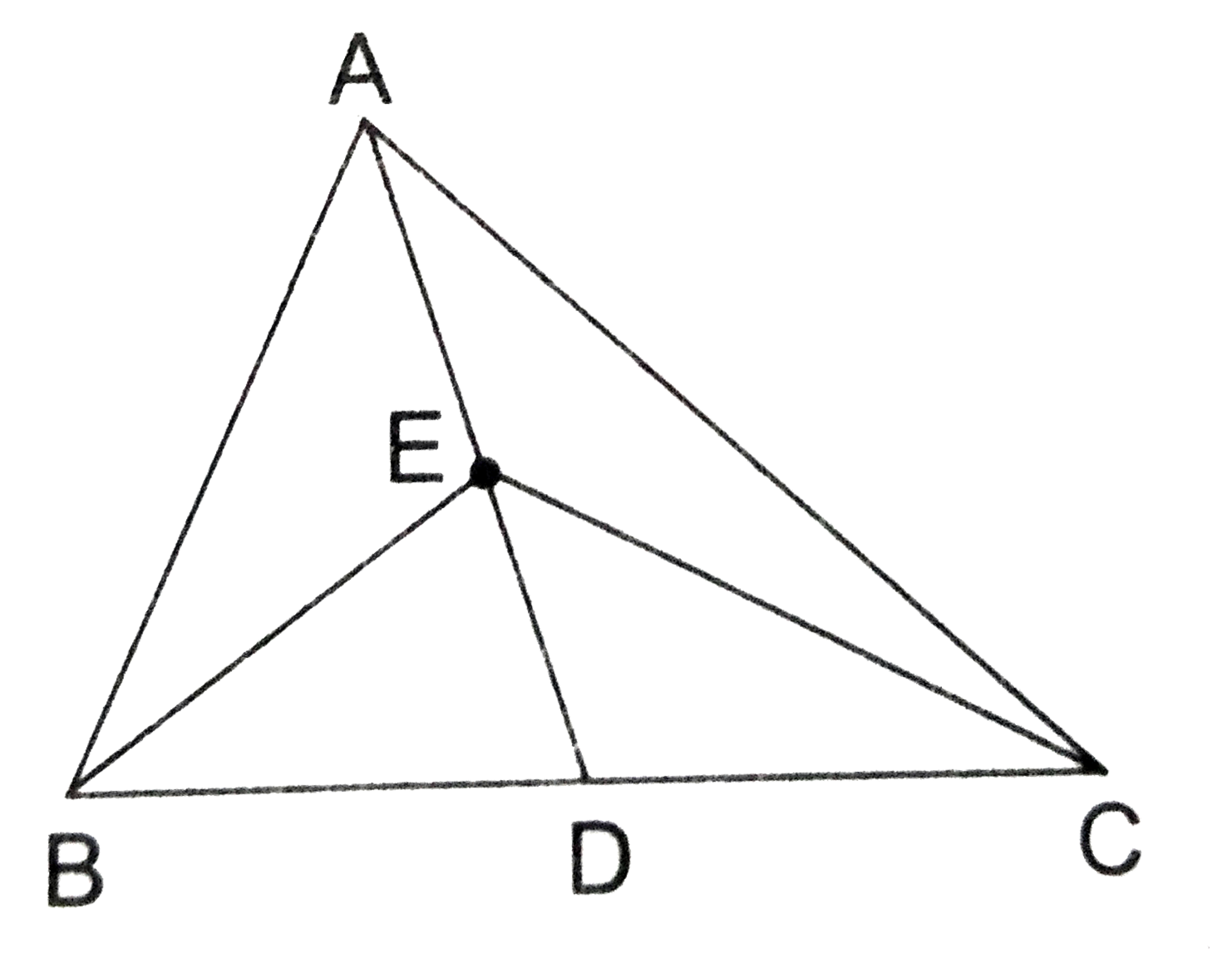
ABC is a triangle in which D is the midpoint of BC and E is the midpoint of AD.
Prove that ar(△BED)=14ar(△ABC).

View SolutionD is the mid-point of side BC of ΔABC and E is the mid-point of BO. If O is the mid-point of AE, then ar(ΔBOE) = 1/k ar(ΔABC). Then k equals
View SolutionIf vertex A of triangle ABC is (3,5) and centroid is (−1,2), then find the midpoint of side BC.
View SolutionIn an equilateral ΔABC,D is the midpoint of AB and E is the midpoint of AC. Then, ar(ΔABC):ar(ΔADE)=?

View SolutionIn a triangle ABC, E is the mid-point of median AD. Show that ar(△BED)=14ar(△ABC).
View Solution