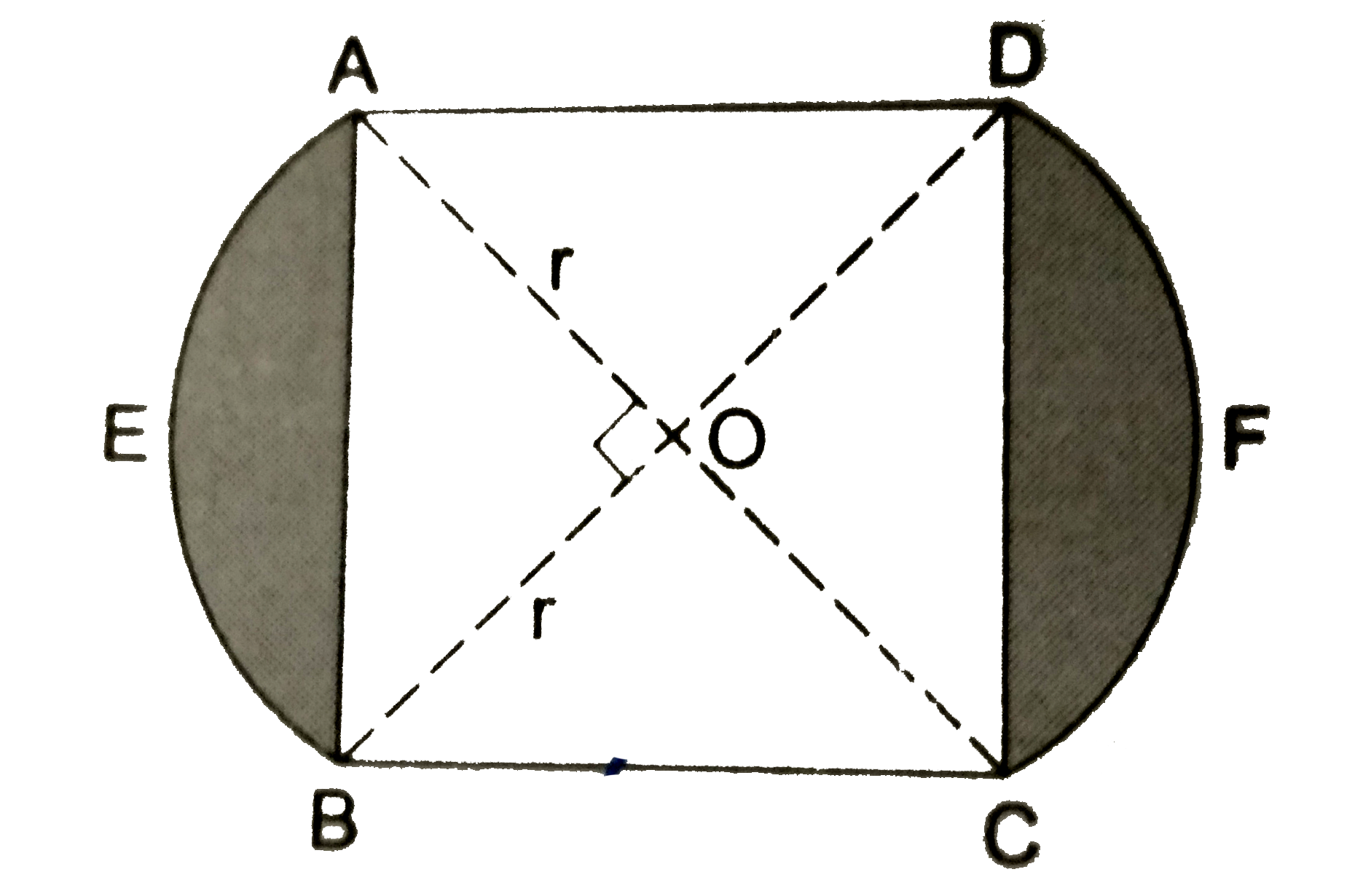
There are two circular flower beds on two sides of a square lawn ABCD of side 56 m. If the centre of each circular flower bed is the point of intersection of the diagonals of the square lawn, find the sum of the areas of the lawn and the flower beds.
Side of square ABCD=56m
AC=BD(diagonals of a square are equal in lengths)
Diagonal of square (AC)=√2×side square
AC=√2×56=56√2
OA=OB=12AC=12(56√2)=28√2
Let OA=OB=r[radius of the sector]
Area of sector OAB=[90∘360∘]πr2
OAB=14×227×(28√2)2=1232
Area of flower bedAB=area of sectorOAB−area of△OAB
⇒1232−12×OB×OA
⇒1232−784=448
Similarly, Area of other flower bedCD=448
Total area=Area of squareABCD+area of flower bedAB+Area of flower bedCD
Total Area=(56×56)+448+448=4032m2.
Topper's Solved these Questions
Similar Questions
In Figure, two circular flower beds have been shown on two sides of a square lawn ABCD of side 56m. If the centre of each circular flower bed is the point of intersection of the diagonals of the square lawn, find the sum of the areas of the lawns and the flower beds.
View SolutionIn the given figure, two circular flower beds have been shown on two sides of a square lawn ABCD of side AB=42m. If the centre of each circular flower bed is the point of intersection O of the diagonals of the square lawn, find
(i) the sum of the areas of the lawn and flower beds,
(ii) the sum of the areas of two flower beds.
View SolutionThe area of a square lawn of side 15 m is
View SolutionIt is proposed to add to a square lawn measuring 58cm on a side, two circalar ends. The centre of each circle is the point of intersection of the diagonals of the square. Find the area of the whole lawn.
View SolutionA square garden ABCD whose Two more circles of side 56 meters. The area has flowers if the flowers are circular Area center diagonals of ABCD Is the point of intersection of the garden and Sum of the area of the flowering area D
View SolutionFind the area of the flower bed (with semicircular ends).

View SolutionFind the area of the flower bed (with semicircular ends).

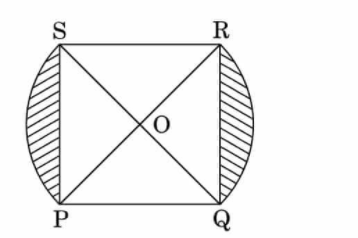
View Solution. In the following figure, PQRS is square lawn with side PQ = 42 metres. Two circular flower beds are there on the sides PS and QR with centre at O, the intersections of its diagonals. Find the total area of the two flower beds (shaded parts).
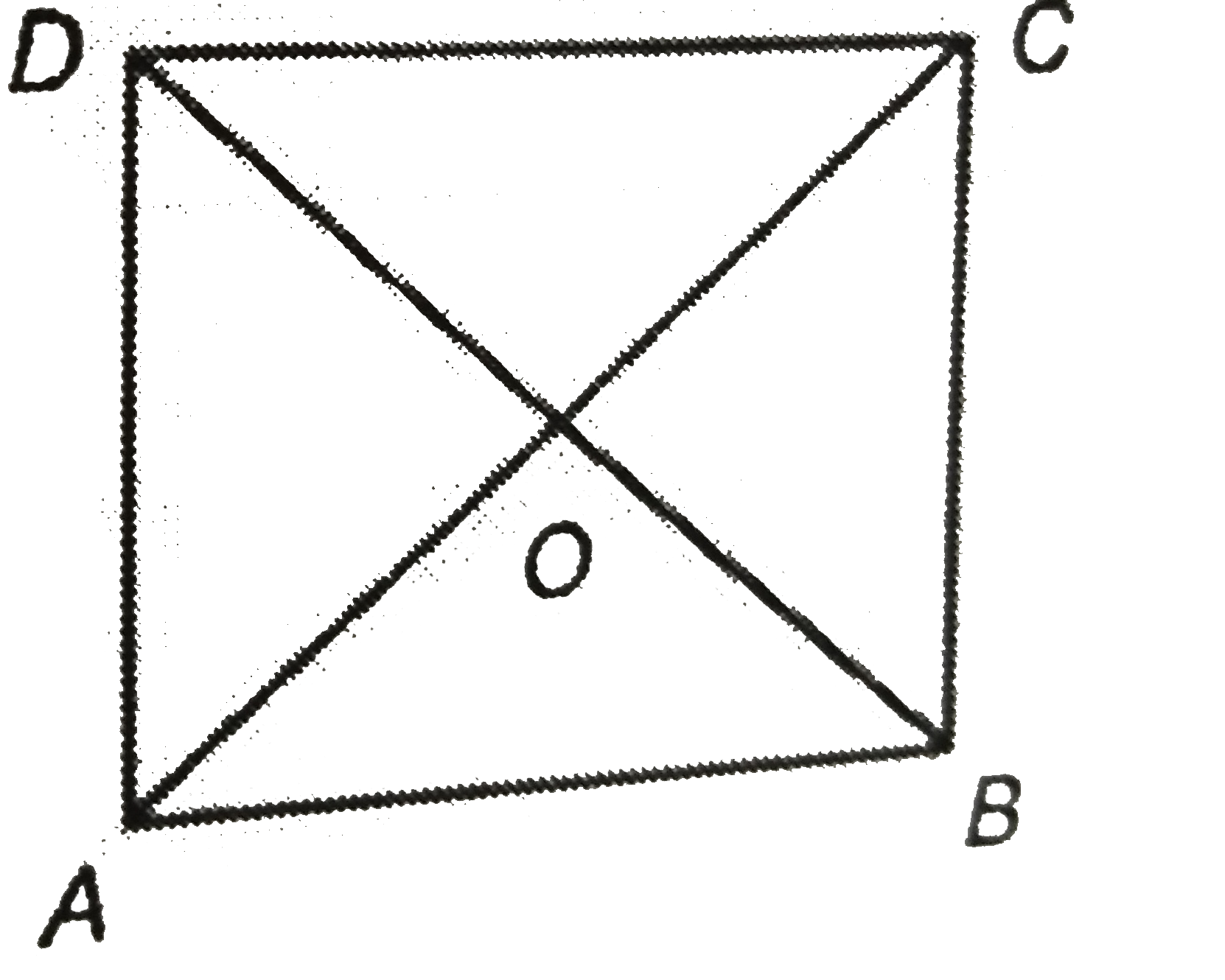
View SolutionIf the sum of the lengths of two diagonals of the given square ABCD is 24 cm, then find the side of the square and the magnitude of AO + OB.
View SolutionThe side of a square exceeds the side of the another square by 4 cm and the sum of the areas of the two squares is 400 sq. cm. Find the dimensions of the squares.
View Solution
