There is a regular hexagon MNOPQR of side 5 cm . aman and ridhima divided it into two different ways . Find the area of this hexagon both ways.
To find the area of the regular hexagon MNOPQR with a side length of 5 cm using two different methods, we can follow these steps:
Method 1: Aman's Method (Dividing into Trapeziums)
1. Identify the shape: The hexagon is divided into two congruent trapeziums.
2. Determine the dimensions of the trapezium:
- The height of each trapezium is given as 4 cm.
- The lengths of the parallel sides are 5 cm (one side of the hexagon) and 11 cm (the other side of the trapezium).
3. Use the trapezium area formula:
The area A of a trapezium can be calculated using the formula:
A=12×(a+b)×h
where a and b are the lengths of the parallel sides, and h is the height.
4. Substitute the values into the formula:
A=12×(5+11)×4
A=12×16×4
A=8×4=32 cm2
5. Calculate the area of the hexagon: Since the hexagon consists of two congruent trapeziums, the total area of the hexagon is:
Area of hexagon=2×Area of one trapezium=2×32=64 cm2
Method 2: Ridhima's Method (Dividing into Triangles and Rectangle)
1. Identify the shape: The hexagon is divided into two congruent triangles (MNO and PQR) and one rectangle (NOPQ).
2. Determine the dimensions:
- The height of each triangle is given as 3 cm.
- The base of each triangle is 8 cm.
- The dimensions of the rectangle are: length = 8 cm, breadth = 5 cm.
3. Calculate the area of the triangles:
The area A of one triangle can be calculated using:
A=12×base×height
A=12×8×3=12 cm2
Since there are two triangles:
Total area of triangles=2×12=24 cm2
4. Calculate the area of the rectangle:
The area A of the rectangle is:
A=length×breadth=8×5=40 cm2
5. Calculate the total area of the hexagon:
Area of hexagon=Area of triangles+Area of rectangle=24+40=64 cm2
Conclusion
In both methods, the area of the hexagon MNOPQR is found to be 64 cm².
---
2. Determine the dimensions of the trapezium:
- The height of each trapezium is given as 4 cm.
- The lengths of the parallel sides are 5 cm (one side of the hexagon) and 11 cm (the other side of the trapezium).
The area A of a trapezium can be calculated using the formula:
A=12×(a+b)×h
where a and b are the lengths of the parallel sides, and h is the height.
A=12×(5+11)×4
A=12×16×4
A=8×4=32 cm2
Area of hexagon=2×Area of one trapezium=2×32=64 cm2
- The height of each triangle is given as 3 cm.
- The base of each triangle is 8 cm.
- The dimensions of the rectangle are: length = 8 cm, breadth = 5 cm.
The area A of one triangle can be calculated using:
A=12×base×height
A=12×8×3=12 cm2
Since there are two triangles:
Total area of triangles=2×12=24 cm2
The area A of the rectangle is:
A=length×breadth=8×5=40 cm2
Area of hexagon=Area of triangles+Area of rectangle=24+40=64 cm2
In both methods, the area of the hexagon MNOPQR is found to be 64 cm².
Topper's Solved these Questions
- MENSURATIONBOOK - NCERT ENGLISHCHAPTER - MENSURATIONEXERCISE - EXERCISE 11.4
8 Videos
- MENSURATIONBOOK - NCERT ENGLISHCHAPTER - MENSURATIONEXERCISE - EXERCISE 11.1
5 Videos
- LINEAR EQUATIONS IN ONE VARIABLEBOOK - NCERT ENGLISHCHAPTER - LINEAR EQUATIONS IN ONE VARIABLEEXERCISE - EXERCISE 2.3
9 Videos
- PLAYING WITH NUMBERSBOOK - NCERT ENGLISHCHAPTER - PLAYING WITH NUMBERSEXERCISE - EXERCISE 16.1
10 Videos
Similar Questions
Knowledge Check
The figure above shows a regular hexagon with sides of length a and a square with sides of length a. If the area of the hexagon is 384 √3 square inches, what is the area, in square inches, of the square?A256B192C64√3D16√3
Construct a regular hexagon of side
(i) 2.5cm
(ii) 3.2cm.
View SolutionA wire shaped to a regular hexagon of side 2cm carries a current of 2A. Find the magnetic field at the cetre of the hexagon.
View SolutionA wire shaped to a regular hexagon of side 2cm carries a current of 2A. Find the magnetic field at the cetre of the hexagon.
View SolutionFind the area of a square whose side is 5cm.
View SolutionA regular hexagon of side 10 cm has a charge 5μC at each of its vertices. Calculate the potential at the center of the hexagon.
View SolutionDraw a circle circumscribing a regular hexagon with side 5 cm.
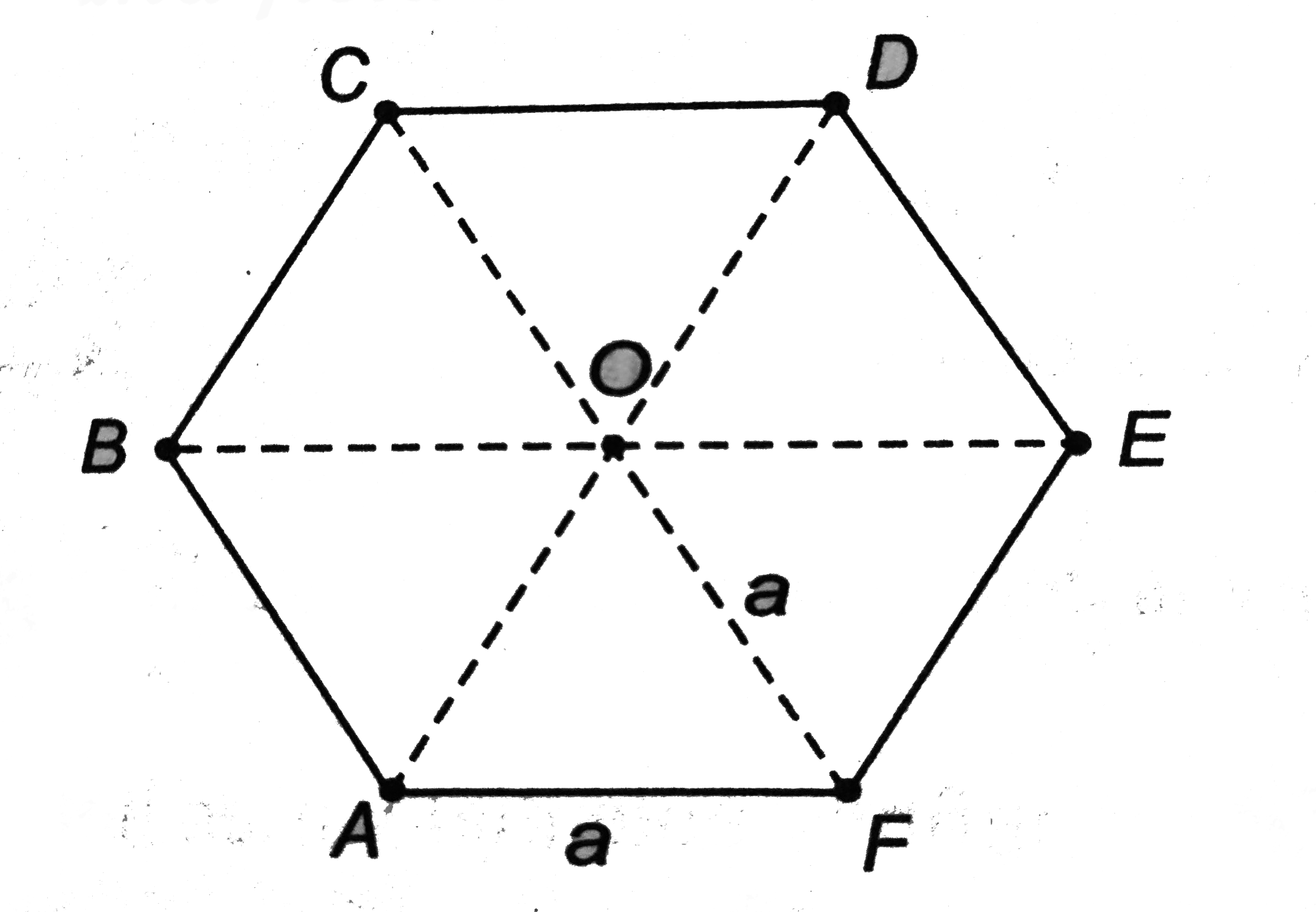
View SolutionFour point masses easch of mass 'm' are placed at four vertieces A, B, C, nd D of a regular hexagon of side 'a' as shown in figure , Find gravitational potential and field strength at the centre O of the hexagon.
 .
.
View Solution
