A wire shaped to a regular hexagon of side 2cm carries a current of 2A. Find the magnetic field at the cetre of the hexagon.
To find the magnetic field at the center of a regular hexagon shaped wire carrying a current, we can follow these steps:
Step 1: Understand the Geometry of the Hexagon
A regular hexagon has six equal sides. Given that each side of the hexagon is 2cm, we can visualize the hexagon and recognize that the center of the hexagon is equidistant from all its sides.
Step 2: Determine the Distance from the Center to a Side
For a regular hexagon, the distance from the center to the midpoint of any side can be calculated using trigonometry. The perpendicular distance (r) from the center to the midpoint of a side can be found as:
\( r = \frac{a \cdot \sqrt{3}}{2} \)
where \( a \) is the length of a side. Here, \( a = 2 \, \text{cm} = 0.02 \, \text{m} \).
Thus,
\( r = \frac{2 \cdot \sqrt{3}}{2} = \sqrt{3} \, \text{cm} = 0.01\sqrt{3} \, \text{m} \)
Step 3: Calculate the Magnetic Field Due to One Side
The magnetic field \( B \) at a distance \( r \) from a long straight wire carrying a current \( I \) is given by the formula:
\( B = \frac{\mu_0 I}{4 \pi r} (\sin \alpha + \sin \beta) \)
For a regular hexagon, the angles \( \alpha \) and \( \beta \) are both \( 30^\circ \) (since the total angle at the center for each side is \( 60^\circ \)). Therefore, \( \sin 30^\circ = \frac{1}{2} \).
Substituting the values:
\( B = \frac{\mu_0 I}{4 \pi r} \left( \sin 30^\circ + \sin 30^\circ \right) = \frac{\mu_0 I}{4 \pi r} \cdot 1 \)
Here, \( I = 2 \, \text{A} \) and \( \mu_0 = 4\pi \times 10^{-7} \, \text{T m/A} \).
Step 4: Substitute the Values
Now substituting the values into the equation:
\( B = \frac{4\pi \times 10^{-7} \cdot 2}{4\pi \cdot 0.01\sqrt{3}} \)
The \( 4\pi \) cancels out:
\( B = \frac{2 \times 10^{-7}}{0.01\sqrt{3}} \)
Step 5: Calculate the Total Magnetic Field
Since there are 6 sides contributing equally to the magnetic field at the center, we multiply the magnetic field due to one side by 6:
\( B_{\text{total}} = 6 \cdot B = 6 \cdot \frac{2 \times 10^{-7}}{0.01\sqrt{3}} \)
\( B_{\text{total}} = \frac{12 \times 10^{-7}}{0.01\sqrt{3}} = \frac{12 \times 10^{-5}}{\sqrt{3}} \)
Step 6: Final Calculation
Now substituting the value of \( \sqrt{3} \approx 1.732 \):
\( B_{\text{total}} = \frac{12 \times 10^{-5}}{1.732} \approx 6.93 \times 10^{-5} \, \text{T} \)
Conclusion
The magnetic field at the center of the hexagon is approximately:
\( B \approx 6.93 \times 10^{-5} \, \text{T} \)
A regular hexagon has six equal sides. Given that each side of the hexagon is 2cm, we can visualize the hexagon and recognize that the center of the hexagon is equidistant from all its sides.
For a regular hexagon, the distance from the center to the midpoint of any side can be calculated using trigonometry. The perpendicular distance (r) from the center to the midpoint of a side can be found as:
\( r = \frac{a \cdot \sqrt{3}}{2} \)
where \( a \) is the length of a side. Here, \( a = 2 \, \text{cm} = 0.02 \, \text{m} \).
Thus,
\( r = \frac{2 \cdot \sqrt{3}}{2} = \sqrt{3} \, \text{cm} = 0.01\sqrt{3} \, \text{m} \)
The magnetic field \( B \) at a distance \( r \) from a long straight wire carrying a current \( I \) is given by the formula:
\( B = \frac{\mu_0 I}{4 \pi r} (\sin \alpha + \sin \beta) \)
For a regular hexagon, the angles \( \alpha \) and \( \beta \) are both \( 30^\circ \) (since the total angle at the center for each side is \( 60^\circ \)). Therefore, \( \sin 30^\circ = \frac{1}{2} \).
\( B = \frac{\mu_0 I}{4 \pi r} \left( \sin 30^\circ + \sin 30^\circ \right) = \frac{\mu_0 I}{4 \pi r} \cdot 1 \)
Here, \( I = 2 \, \text{A} \) and \( \mu_0 = 4\pi \times 10^{-7} \, \text{T m/A} \).
Now substituting the values into the equation:
\( B = \frac{4\pi \times 10^{-7} \cdot 2}{4\pi \cdot 0.01\sqrt{3}} \)
The \( 4\pi \) cancels out:
\( B = \frac{2 \times 10^{-7}}{0.01\sqrt{3}} \)
Since there are 6 sides contributing equally to the magnetic field at the center, we multiply the magnetic field due to one side by 6:
\( B_{\text{total}} = 6 \cdot B = 6 \cdot \frac{2 \times 10^{-7}}{0.01\sqrt{3}} \)
\( B_{\text{total}} = \frac{12 \times 10^{-7}}{0.01\sqrt{3}} = \frac{12 \times 10^{-5}}{\sqrt{3}} \)
Now substituting the value of \( \sqrt{3} \approx 1.732 \):
\( B_{\text{total}} = \frac{12 \times 10^{-5}}{1.732} \approx 6.93 \times 10^{-5} \, \text{T} \)
The magnetic field at the center of the hexagon is approximately:
\( B \approx 6.93 \times 10^{-5} \, \text{T} \)
Topper's Solved these Questions
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Check point
54 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Taking it together
75 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 Subjective
5 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Video
Similar Questions
Knowledge Check
Six point charges are arrange at the vertices of a regular hexagon of side length a (shown in figure).
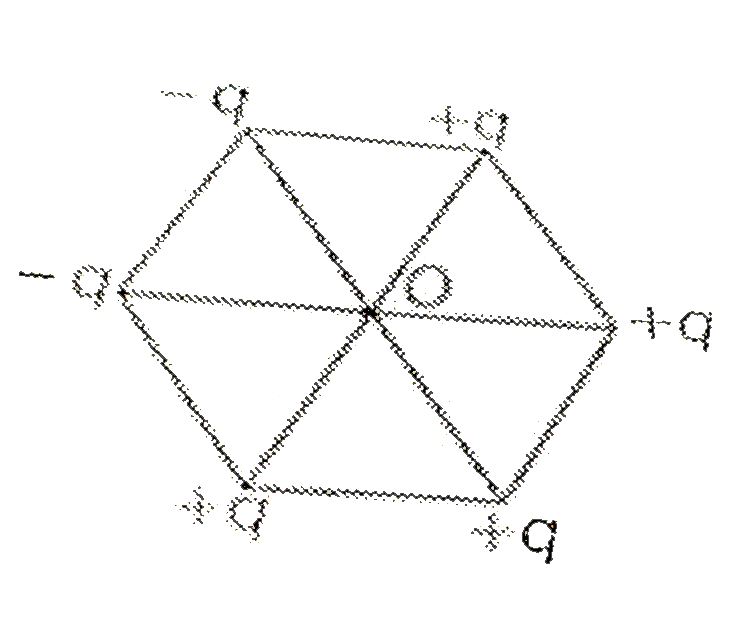
Find the magnitude of electric field at the centre of regular hexagon.A−qB−q6C+1.83qD−1.83qA hexagon of side 8 cm has a charge 4μC at each of its vertices. The potential at the centre of the hexagon is
A2.7×106VB7.2×1011VC2.5×1012VD3.4×104V
A regular polygon of n sides is formed by bending a wire of total length 2πr which carries a current i. (a) Find the magnetic field B at the centre of the polygon. (b) By letting n→∞ , deduce the expression for the magnetic field at the centre of a circular current.
View SolutionA regular polygon of n sides is formed by bending a wire of total length 2πr which carries a current i. (a) Find the magnetic field B at the centre of the polygon. (b) By letting n→∞ , deduce the expression for the magnetic field at the centre of a circular current.
View SolutionA regular polygon of n sides is formed by bending a wire of total length 2πr which carries a current i. (a) Find the magnetic field B at the centre of the polygon. (b) By letting n→∞ , deduce the expression for the magnetic field at the centre of a circular current.
View SolutionA loop in the shape of an equilateral triangle triangle of side a carries a current I as shown in the figure.Find out the magnetic field at the centre C of the triangle.
View SolutionSix point charges are placed at the vertices of a hexagon of side 1 m as shown in figure. Net electric field at the centre of the hexagon is
View SolutionA regular hexagon of side 10 cm has a charge 5μC at each of its vertices. Calculate the potential at the center of the hexagon.
View Solution