To warn ships for underwater rocks, a lighthouse spreads a red coloured light over a sector of angle 80oto a distance of 16.5 km. Find the area of the sea over which the ships are warned.
To find the area of the sea over which ships are warned by the lighthouse, we can use the formula for the area of a sector of a circle. The formula is:
Area=θ360×πr2
where:
- θ is the angle of the sector in degrees,
- r is the radius of the sector.
1. Identify the given values:
- Angle, θ=80∘
- Radius, r=16.5 km
2. Substitute the values into the formula:
Area=80360×π×(16.5)2
3. Simplify the fraction:
80360=836=29
4. Calculate (16.5)2:
(16.5)2=272.25
5. Substitute back into the area formula:
Area=29×π×272.25
6. Use π≈227 for calculation:
Area=29×227×272.25
7. Calculate the area:
- First, calculate 2×22×272.259×7:
=12000.363≈190.00 km2
8. Final result:
The area of the sea over which the ships are warned is approximately 190.00 km2.
- θ is the angle of the sector in degrees,
- r is the radius of the sector.
- Angle, θ=80∘
- Radius, r=16.5 km
Area=80360×π×(16.5)2
80360=836=29
(16.5)2=272.25
Area=29×π×272.25
Area=29×227×272.25
- First, calculate 2×22×272.259×7:
=12000.363≈190.00 km2
The area of the sea over which the ships are warned is approximately 190.00 km2.
Topper's Solved these Questions
- AREA RELATED TO CIRCLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA RELATED TO CIRCLESEXERCISE - Exercise 12 A
24 Videos
- AREA RELATED TO CIRCLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA RELATED TO CIRCLESEXERCISE - Exercise 12 B
32 Videos
- AREA RELATED TO CIRCLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA RELATED TO CIRCLESEXERCISE - Revision Exercise Long Answer Question
5 Videos
- ARITHMETIC PROGRESSIONBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Revision Exercise Long Answer Question
5 Videos
Similar Questions
To warn ships for underwater rocks, a lighthouse spreads a red coloured light over a sector of angle 80∘to a distance of 16.5 km. Find the area of the sea over which the ships are warned.
View SolutionTo warn ships for underwater rocks, a light house throws a red coloured light over a sector of 80o angle to a distance of 16.5 km. Find the area of the sea over which the ships are warned.
View Solution
Knowledge Check
A cargo ship is 4.2 miles from a lighthouse, and a fishing boat is 5.0 miles from the lighthouse, as shown below. The angle between the straight lines from the lighthouse to the 3 vessels is 5∘. The approximate distance in miles, from the cargo ship to the fishing boat is given by which of the following expressions?
(Note: The law of cosines states that for any triangle with vertices A, B and C adn the sides opposite those vertices with length a, b, and c, respectively. c2=a2+b2−2abcosC).
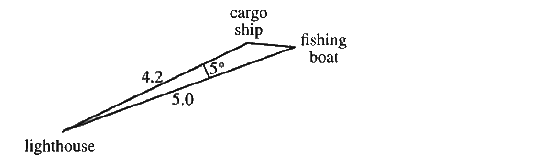 A√(5.0)2−(4.2)2B√(4.2)2+(5.0)2−2⋅4.2⋅5.0cos5∘C√(4.2)2+(5.0)2+2⋅4.2⋅5.0cos5∘D√(4.2)2+(5.0)2−2⋅4.2⋅5.0cos85∘
A√(5.0)2−(4.2)2B√(4.2)2+(5.0)2−2⋅4.2⋅5.0cos5∘C√(4.2)2+(5.0)2+2⋅4.2⋅5.0cos5∘D√(4.2)2+(5.0)2−2⋅4.2⋅5.0cos85∘
A driver having a definite reaction time is capable of stopping his car over a distance of 30 m on seeing a red traffic signal, when the speed of the car is 72 km/hr andover a distance of 10 m when the speed is 36 km/hr. Find the distance over which he can stop the car if it were running at a speed of 54 km/hr. Assume that his reaction time and the deceleration of the car remains same in all the three cases.
View SolutionTwo ships are there in the sea on either side of a light house in such a way that the ships and the light house are in the same straight line. The angles of depression of two ships are observed from the top of the light house are 60∘ and 45∘ respectively. If the height of the light house is 200 m, find the distance between the two ships. (Use √3=1.73)
View SolutionFrom the top of a 75m high lighthouse from the sea level the angles of depression of two ships are 30∘ and 45∘. If the two ships are on the opposite sides of the light house then find the distance between the two ships.
View SolutionAs observed from the top of a light house, 100m above sea level, the angle of depression of a ship, sailing directly towards it, changes from 30o to 45o . Determine the distance travelled by the ship during the period of observation.
View SolutionA ship is moving at a constant speed of 10km/hr in the direction of the unit vector ˆi. Initially. Its position vector, relative to a fixed origin is 10(−ˆi+ˆj) where ˆi & ˆj are perpendicular vectors of length 1 km. Find its position vector relative to the origin at time t hours later. A second ship is moving with constant speed ukm/hr parallele to the vector ˆi+2ˆj and is initially at the origin
(i) If u=10√5km/h. Find the minimum distance between the ships and the corresponding value of t
(ii) Find the value of u for which the shipd are on a collision course and determine the value of t at which the collision would occur if no avoiding action were taken.
View SolutionA field is in the form of a rectangle of length 18m and width 15m. A pit, 7.5m long, 6m broad and 0.8m deep, is dug in a corner of the field and the earth taken out is spread over the remaining area of the field. Find cut the extent to which the level of the field has been raised.
View SolutionAn agricultural field is in the form of a rectangle of length 20m and width 14m. A pit 6mlong,3mwideand2.5mdeep is dug in a corner of the field and the earth taken out of the pit is spread uniformly over the remaining area of the field. Find the extent to which the level of the field has been raised.
View Solution
