Triangle ABC is right angled at A. The circle with centre A and radius AB cuts BC and AC internally at D and E respectively. If BD=20 and DC=16 then the length AC equals Solution in Bengali
6√21
6√26
30
32
The correct Answer is:B
b2+r2=(36)2 (1)
Also, CD.CB=CE.CX
∴16.36=(b−r)(b+r)
∴b2−r2=16×36 (2)
From (1) and (2)
2b2+36(36+16)=36×52
⇒b=6√26
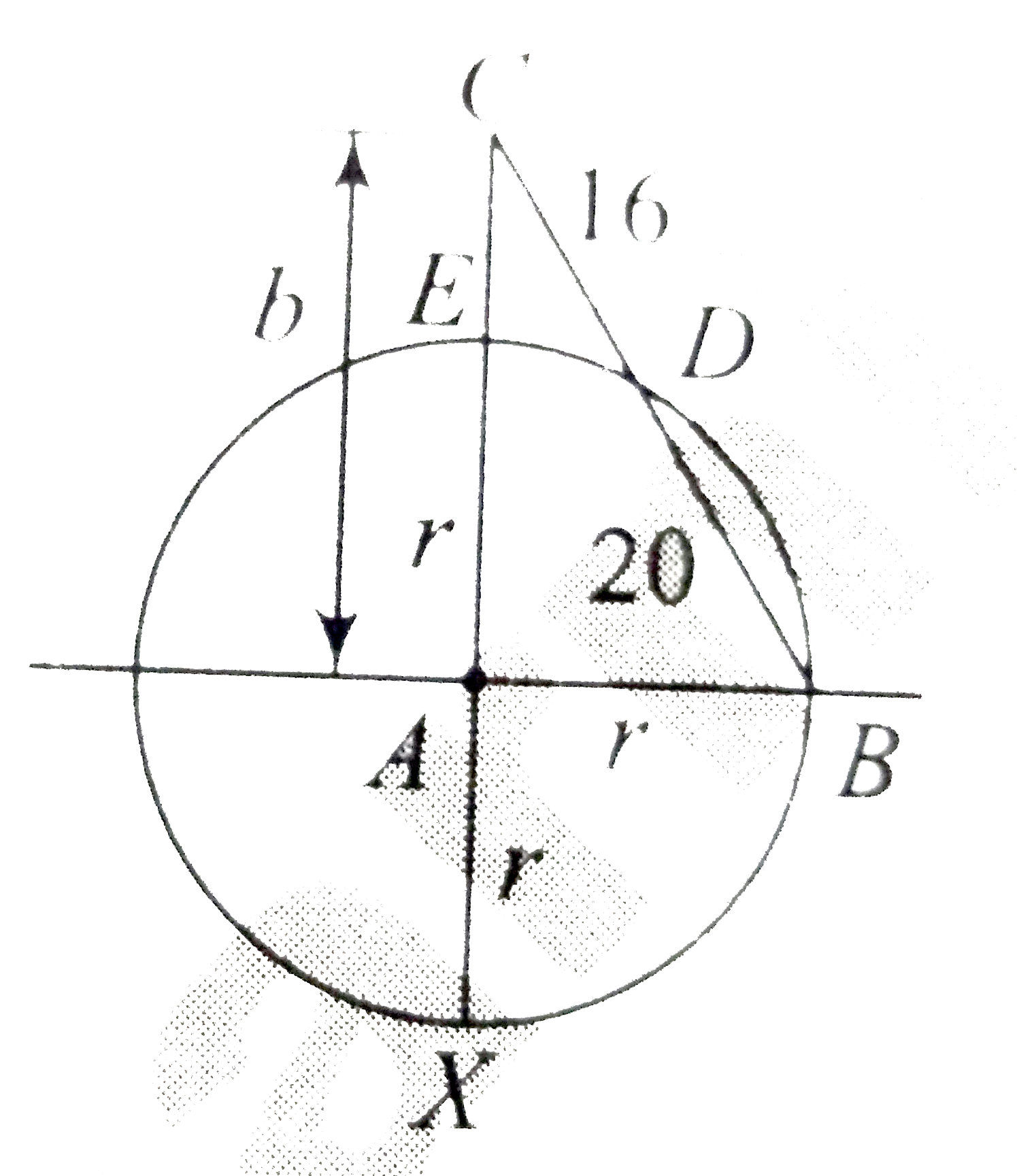
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Multiple Correct Answers Type9videos
CIRCLES
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type8videos
CIRCLES
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - For problems 3 and 42videos
CIRCLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - COMPLEX NUMBERSEXERCISE - MULTIPLE CORRECT ANSWER TYPE6videos
COMPLEX NUMBERS
Similar Questions
The line 3x+6y=k intersects the curve 2x2+3y2=1 at points AandB . The circle on AB as diameter passes through the origin. Then the value of k2 is__________
05:52View Solution
In the diagram as shown, a circle is drawn with centre C(1,1) and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals θ where 0<θ<π2.
Coordinate of Q is04:46View SolutionPARAGRAPH X Let S be the circle in the xy -plane defined by the equation x2+y2=4. (For Ques. No 15 and 16) Let E1E2 and F1F2 be the chords of S passing through the point P0(1, 1) and parallel to the x-axis and the y-axis, respectively. Let G1G2 be the chord of S passing through P0 and having slope −1 . Let the tangents to S at E1 and E2 meet at E3 , the tangents to S at F1 and F2 meet at F3 , and the tangents to S at G1 and G2 meet at G3 . Then, the points E3, F3 and G3 lie on the curve x+y=4 (b) (x−4)2+(y−4)2=16 (c) (x−4)(y−4)=4 (d) xy=4
01:14View SolutionLet z1 and z2 be two distinct complex numbers and z=(1−t)z1+tz2, for some real number t with 0<t<1 and i=√−1. If arg(w) denotes the principal argument of a non-zero compolex number w, then
05:26View SolutionTriangle ABC is right angled at A. The circle with centre A and radius AB cuts BC and AC internally at D and E respectively. If BD=20 and DC=16 then the length AC equals (A) 6sqrt21 (B) 6sqrt26 (C) 30 (D)32
02:35View SolutionLet ABC be a right triangle with length of side AB=3 and hypotenuse AC=5. If D is a point on BC such that BDDC=ABAC, then AD is equal to
05:12View SolutionABC is a right triangle right-angled at A and AD⊥BC . Then, BDDC= (ABAC)2 (b) ABAC (c) (ABAD)2 (d) ABAD
03:54View SolutionIf a circle is inscribed in right angled triangle ABC with right angle at B, show that the diameter of the circle is equal to AB+BC−AC.
03:03View SolutionABC is a right angled triangle of which A is the right angle, BD is drawn perpendicular to BC meets CA produced in D. If AB = 12, AC = 16, BC = 20, then BD =
02:07View Solutionकिसी △ABC में, D, भुजा BC का मध्य बिंदु इस प्रकार है कि BDDC=ABAC सिद्ध कीजिए कि AD, ∠A का अर्द्धक है |
04:05View SolutionLet ABC be a right triangle with length of side AB=3 and hyotenus AC=5. If D is a point on BC such that BDDC=ABAC, then AD is equal to
04:15View SolutionThe incircle of an isosceles triangle ABC in which AB=AC, touches the sides BC, CA, and AB at D, E, and F respectively. Prove that BD=DC.
View SolutionTriangle ABC is right angled at A. The circle with centre A and radius AB cuts BC and AC internally at D and E respectively. If BD=20 and DC=16 then the length AC equals (A) 6sqrt21 (B) 6sqrt26 (C) 30 (D)32
02:05View SolutionABC is a right angled triangle of which A is the right angle, BD is drawn perpendicular to BC meets CA produced in D. If AB = 12, AC = 16, BC = 20, then BD =
05:19View Solutionमाना ABC एक समकोण त्रिभुज है तथा भुजा AB की लम्बाई 3 एवं विकर्ण AC की लम्बाई 5 है यदि D, BC पर एक बिन्दु इस प्रकार है कि BDDC=ABAC है तो AD का मान है
03:06View Solutionसमकोण त्रिभुज ABC कोण B पर समकोण है, तथा एक अंत: वृत्त भुजा AB, BC व AC को क्रमश F, E व D पर स्पर्श करता है, यदि BD, AC पर लम्ब है, तो AF व FB का अनुपात ज्ञात कीजिये।
06:56View Solution

