Let ABC be a right triangle with length of side AB=3 and hyotenus AC=5. If D is a point on BC such that BDDC=ABAC, then AD is equal to
4√33
3√52
4√53
5√34
The correct Answer is:B
To solve the problem step-by-step, we will follow the logic presented in the video transcript.
Step 1: Identify the triangle and given values
We have a right triangle ABC where:
- AB=3 (one leg)
- AC=5 (hypotenuse)
Step 2: Find the length of side BC
Using the Pythagorean theorem:
AB2+BC2=AC2
Substituting the known values:
32+BC2=52
9+BC2=25
BC2=25−9=16
BC=√16=4
Step 3: Set up the ratio BDDC
We are given that:
BDDC=ABAC=35
Let BD=3x and DC=5x. Then, we can express BC as:
BD+DC=BC⟹3x+5x=4⟹8x=4⟹x=12
Thus:
BD=3x=3⋅12=32
DC=5x=5⋅12=52
Step 4: Find AD using the Pythagorean theorem in triangle ABD
Now we will use the Pythagorean theorem again in triangle ABD:
AD2=AB2+BD2
Substituting the known values:
AD2=32+(32)2
AD2=9+94
To combine these, convert 9 into a fraction:
9=364
Thus:
AD2=364+94=454
Taking the square root:
AD=√454=√452=3√52
Final Answer
Thus, the length of AD is:
AD=3√52
We have a right triangle ABC where:
- AB=3 (one leg)
- AC=5 (hypotenuse)
Using the Pythagorean theorem:
AB2+BC2=AC2
Substituting the known values:
32+BC2=52
9+BC2=25
BC2=25−9=16
BC=√16=4
We are given that:
BDDC=ABAC=35
Let BD=3x and DC=5x. Then, we can express BC as:
BD+DC=BC⟹3x+5x=4⟹8x=4⟹x=12
Thus:
BD=3x=3⋅12=32
DC=5x=5⋅12=52
Now we will use the Pythagorean theorem again in triangle ABD:
AD2=AB2+BD2
Substituting the known values:
AD2=32+(32)2
AD2=9+94
To combine these, convert 9 into a fraction:
9=364
Thus:
AD2=364+94=454
Taking the square root:
AD=√454=√452=3√52
Thus, the length of AD is:
AD=3√52
Topper's Solved these Questions
- PROPERTIES AND SOLUTION OF TRIANGLES Book:ARIHANT MATHS ENGLISHChapter:PROPERTIES AND SOLUTION OF TRIANGLES Exercise:Exercise (More Than One Correct Option Type Questions)
Explore 23 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES Book:ARIHANT MATHS ENGLISHChapter:PROPERTIES AND SOLUTION OF TRIANGLES Exercise:Exercise (Statement I And Ii Type Questions)
Explore 11 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES Book:ARIHANT MATHS ENGLISHChapter:PROPERTIES AND SOLUTION OF TRIANGLES Exercise:PROPERTIES AND SOLUTIONS OF TRIANGLES EXERSISE 1: SINGLE OPTION CORRECT TYPE QUESTIONS
Explore 1 Video
- PRODUCT OF VECTORSBook:ARIHANT MATHS ENGLISHChapter:PRODUCT OF VECTORSExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 51 Videos
- SEQUENCES AND SERIESBook:ARIHANT MATHS ENGLISHChapter:SEQUENCES AND SERIESExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 38 Videos
Similar Questions
In ΔABC,AB=AC and D is a point in BC so that BD=CD. Prove that AD bisects ∠BAC.
View SolutionABC is a triangle in which AB=ACandD is a point on AC such that BC2=AC×CD.Prove that BD=BC.
View SolutionIn triangle ABC, D is a point in side AB such that AB = 4AD and E is a point in AC such that AC = 4AE. Show that BC : DE = 4:1
View SolutionABC is a triangle in which AB = AC and D is any point on BC. Prove that:
AB2−AD2=BD.CD
View SolutionIn triangle ABC, angle A=90∘,CA=AB and D is a point on AB produced. Prove that:
DC2−BD2=2AB.AD.
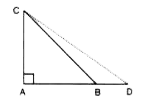
View SolutionIn Fig. 3, ABC is a right triangle, right angled at C and D is the mid-point of BC. Prove that AB2=4AD2−3AC2.
View SolutionABC is an equilateral triangle. Length of each side is 'a' and centroid is point O. Find
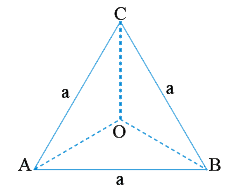
If ∣∣∣−−→AB+−−→BC+−−→AC∣∣∣=na then n = ?
View SolutionABC is a right triangle with AB = AC.If bisector of ∠A meet BC at D then prove that BC =2 AD .
View SolutionABC is an isosceles triangle with AB = AC = 2a and BC = a . If AD⊥BC, find the length of AD .
View SolutionIn a right-angled triangle ABC,∠ABC=90∘ and D is mid-point of AC. Prove that BD=12AC.
View Solution
