Two chords AB and AC of a circle subtends angles equal to 90∘and150∘, respectively at the centre. Find∠BAC, if AB and AC lie on the opposite sides of the centre.
In ΔBOA,OB=OA [both are the radius of circle]
∴∠OAB=∠OBA…(i)
[angles opposite to equal sides are equal]
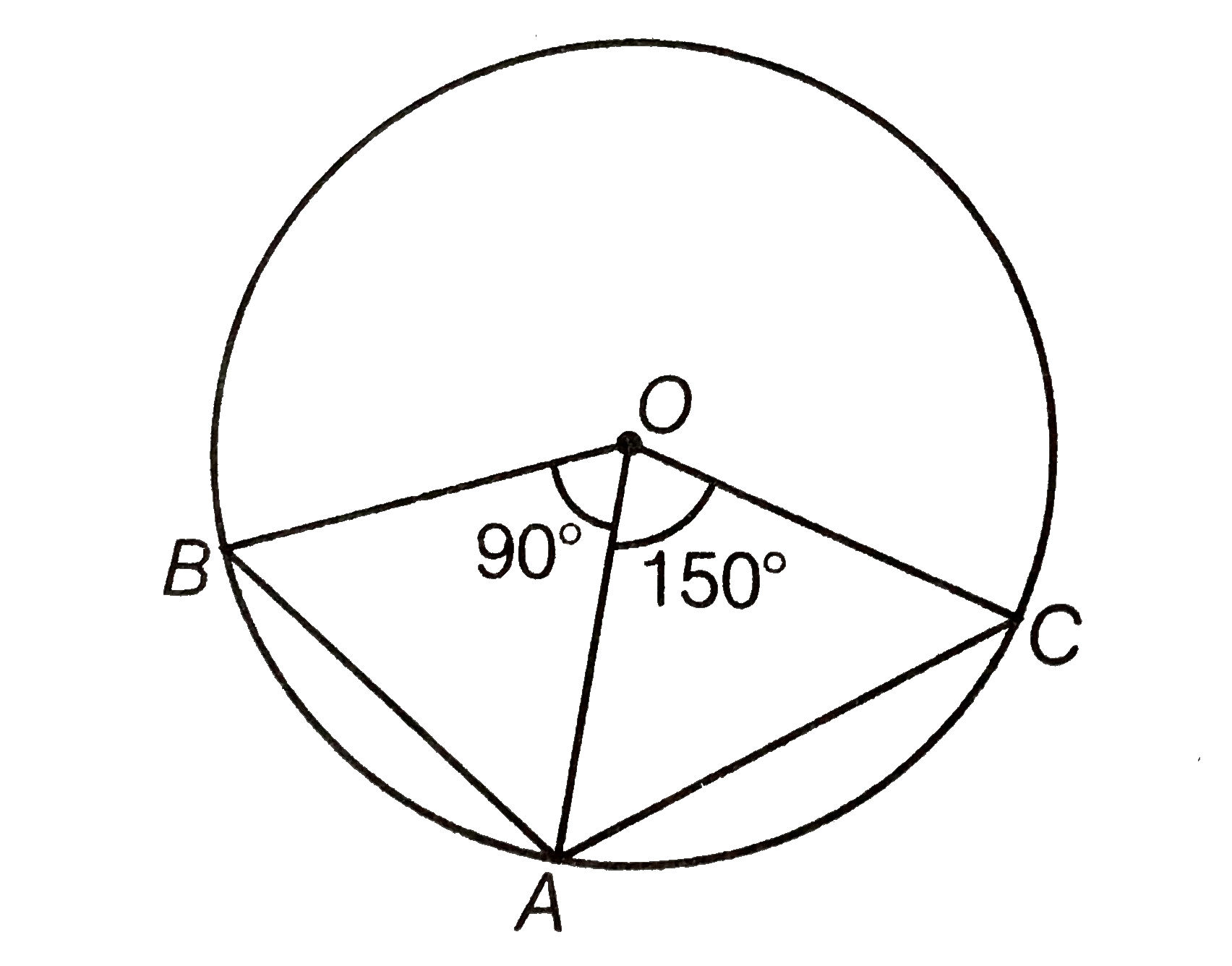
In ΔOAB,∠OBA+∠OAB+∠AOB=180∘ [by angle sum property of a triangle]
⇒∠OAB+∠OAB+90∘=180∘ [from Eq. (i)]
⇒2∠OAB=180∘−90∘
⇒∠OAB=90∘2=45∘
Now, in ΔAOC,AO=OC [both are the redius of a circle]
∴∠OCA=∠OAC...(ii)
[angles opposite to equal sides are equal]
Also, ∠AOC+∠OAC+∠OCA=180∘ [by angle sum property of a triangle]
⇒150∘+2∠OAC=180∘ [from Eq. (ii)]
⇒2∠OAC=180∘−150∘
⇒2∠OAC=30∘
⇒∠OAC=15∘
∴∠BAC=∠OAB+∠OAC=45∘+15∘=60∘
Topper's Solved these Questions
- CIRCLESBOOK - NCERT EXEMPLARCHAPTER - CIRCLESEXERCISE - Exercise 10.4
2 Videos
- Areas of Parallelograms and TrianglesBOOK - NCERT EXEMPLARCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Areas Of Parallelograms And Triangles
34 Videos
- CONSTRUCTIONSBOOK - NCERT EXEMPLARCHAPTER - CONSTRUCTIONSEXERCISE - Long Answer Type Questions
5 Videos
Similar Questions
Equal chords of a circle subtend equal angles at the centre.
View SolutionEqual chord of circle subtends equal angle on centre.
View SolutionLet p and q be the length of two chords of a circle which subtend angles 36∘and60∘ respectively at the centre of the circle . Then , the angle (in radian) subtended by the chord of length p + q at the centre of the circle is (use π=3.1 )
View SolutionProve that equal chords of a circle subtend equal angles at the centre.
View SolutionEqual chords of congruent circles subtend equal angles at the centre.
View SolutionEqual chords of congruent circles subtend equal angles at the centre.
View SolutionState and prove that :
Theorem 10.1 : Equal chords of a circle subtend equal angles at the centre
View SolutionTwo chords AB and AC of a circle are equal. Prove that the centre of the circle lies on the angle bisector of ∠BAC.
View SolutionIn a circle of radius 5 cm, AB and CD are two parallel chords of lengths 8 cm and 6 cm respectively. Calculate the distance between the chords if they are
(i) on the same side of the centre.
(ii) on the opposite sides of the centre.
View SolutionTwo chord AB and AC of a circle are equal. Prove that the centre of a circle lies on the angle bisector of ∠BAC
View Solution
