Two chords AC and BD of a circle intersect each other at the point O. If two tangents drawn at the points A and B intersect each other at the point P and two tangents drawn at the points C and D intersect at the point Q, prove that ∠P+∠Q=2∠BOC.[GP−X] Solution in Bengali
In the circel with centre O', two chords AC and BD intersect each other at O. Two tangents PAS and PBT drawn at the points A and B respectively intersect each oter at P. Again, the tangents QCN and QDM drawn at C and D respectively intersect each other at Q.
To prove : ∠P+∠Q=2∠BOC.
Construction : Let us join O.' A, O', D, A, B and C, D.
Proof : From example 8 above, we get
P=2∠BAO'andQ=2∠DCO' ltbr =2(∠BAQ'+∠DCO')
=2(∠BAC+∠CAO'+∠DCO')[∵BAO'=∠BAC+∠CAO']
=2(∠BDC+∠ACO'+∠DCO')
=2(∠BDC+∠ACD[∵∠ACO'+∠DCO'=∠ACD]
=2(∠ODC+∠OCD([∵∠BDC=∠OBC,∠ACD=∠OCD]
=2∠BOC[∵inΔCOD externla ∠BOC= internally opposite(∠ODC+∠OCD]
Hence ∠P+∠Q=2∠BOC (Proved)

Topper's Solved these Questions
- BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO TANGENT IN A CIRCLE EXERCISE - EXERCISE 4.120videos
THEOREMS RELATED TO TANGENT IN A CIRCLE
- BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO TANGENT IN A CIRCLE EXERCISE - EXERCISE 4.223videos
THEOREMS RELATED TO TANGENT IN A CIRCLE
- BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXERCISE 2.3 (Long Answer Type Questions)14videos
THEOREMS RELATED TO ANGLES IN A CIRCLE
- BOOK - CALCUTTA BOOK HOUSECHAPTER - TRIGONOMETRIC RATIOS AND TRIGONOMETRIC IDENTITIES EXERCISE - EXERCISE66videos
TRIGONOMETRIC RATIOS AND TRIGONOMETRIC IDENTITIES
Similar Questions
PR and PS are two tangents drawn from a extental point P of the Circle with centre at O. If PR=8cmand∠RPO=60∘, then the length of PS=
04:59View SolutionThe distance of the point from the centre of a circle with diameter of 16 cm is 17 cm. Then the length of the tangent from the point to the circle is
02:46View SolutionProve that angle in the segment of a circle which is greater than a semi-circle is an acute angle.
03:23View SolutionIf tanθ=pq, what is the value of psecθ−q cosecθpsecθ+q cosecθ=
07:33View SolutionTwo circles intersect each other at the points P and Q. Two straight lines through P and Q intersect one circle at the points A and C and the other circle at B and D. Prove the AC|| BD
04:49View SolutionP केंद्र वाले, वृत्त के व्यास AB के अंतिम बिन्दुओ पर दो स्पर्श रेखाएं खींची गई। यदि बिंदु C से वृत्त पर खींची गई स्पर्श रेखा, अन्य दो स्पर्श रेखाओ को Q तथा R पर प्रतिछेदित करती है। ∠QPR का मान ज्ञात करे?
07:47View SolutionTwo circles intersect each other at point P and Q. Secants drawn through p and Q intersect the circles at points A,B and D,C
Prove that :∠ADC+∠BCD=180∘
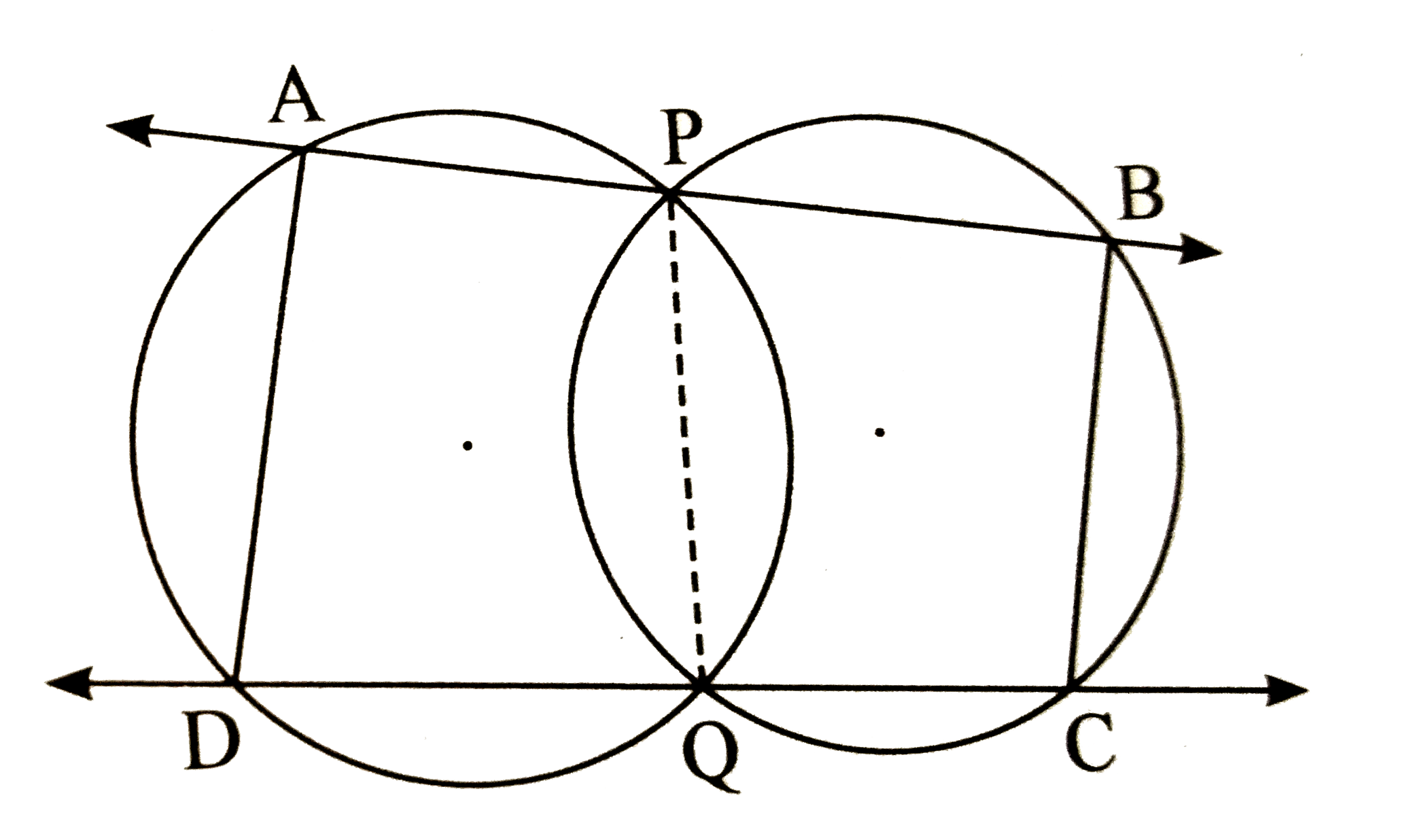 06:15View Solution
06:15View SolutionTwo chords AB and CD of a circle with centre O intersect each other at the point P. prove that AOD+∠BOC=2∠PBC. If ∠BOC are supplementary to each other, then prove that the two chords are perpendicular to each other.
08:30View SolutionAnkita drew two circles which intersect each other at the points P and Q. Through the point P two straight lines are draw so that they intersect one of the circle at the points. A and B and the ohte circle at the points C and D respectively. Prove that ∠AQC=∠BQD.
06:34View SolutionTwo circles intersect each other at the points P and Q. Two straight lines through P and Q intersect on circle at the points A and C and the other circle at B and D . Prove that AC||BD.
05:38View SolutionTwo radii OA and OB of a circle with centre O are perpendicular to each other. If two tangents are drawn at the point A and B intersect each other at the point T, prove that AB=OT and they bisect each other at a ridght angle.
02:06View SolutionP is any point on diameter of a circle with centre O.A perpendicular drawn on diameter at the point O intersects the point O intersects the circle at the point Q. Extended QP intersects the circle at the point R.A tangent drawn at the point R intersects extended OP at the point S. Prove theat SP=SR.[GP−X]
09:01View SolutionQR is a chord of the circle with centre O. Two tangents drawn at eh points Q and R intersect each other at the point P. If QM is a diameter, prove that ∠QPR=2∠RQM[GP−X]
04:30View SolutionPQ is a diameter. The tangent drawn at the point R, intersects the two tangents drawn at the points P and Q at the points A and B respectively. Prove that ∠AOB is a right angle.
06:31View SolutionTwo tangents drawn at the point A and B on a circle intersect each other at the point P. If ∠APB=60∘, then ∠PAB=
03:23View Solution

