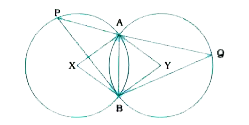
Two congruent circles intersect each other at points A and B. Through A any linesegment PAQ is drawn so that P, Q lie on the two circles. Prove that BP = BQ.
Let point C and D be the centres of the two congruent circles.
Let AB be the common chord.
arcAEB=arcAFB (arcs of congruent chords of congruent circles)
∠APB=∠AQB (angles subtended by congruent arcs)
In △BPQ,
∠APB=∠AQB
Thus, ∠QPB=∠PQB
From converse of isosceles triangle theorem
BQ=BP
Similar Questions
Two congruent circles intersect each other at points A and B. Through A any linesegment PAQ is drawn so that P, Q lie on the two circles. Prove that BP = BQ.
View SolutionTwo congruent circles intersect each other at points A and B. Through A any line segment PAS is drawn so that P, Olie on the two circles. Prove that BP = BQ.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two circles intersect each other at P and Q. PA and PB are two diameters. Then ∠AQB is
A120∘B135∘C160∘D180∘
Two circles intersect each other at point P an Q. If PA and PB are two diameter then find ∠AQB.
View SolutionIn figure, two circles intersect each other at points S and R. Their common tangent PQ touches the circle at points P,Q. Prove that, ∠PRQ+∠PSQ=180∘.
 View Solution
View SolutionIn the figure, two circles intersect each other at points A and B. AP and AQ are the diameters of these circles. Prove that PBQ is a straight line.
 View Solution
View SolutionTwo circles intersect each other at the points P and Q. Two straight lines through P and Q intersect one circle at the points A and C and the other circle at B and D. Prove the AC|| BD
View SolutionThe congruent circles with centres Oand O' intersect at two points A and B. Then, ∠AOB=∠AO'B.
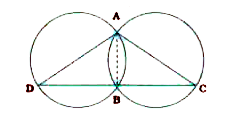
View SolutionTwo circles intersect at two points A and B . AD and AC are diameters to the two circles .Prove that B lies on the line segment DC.
 View Solution
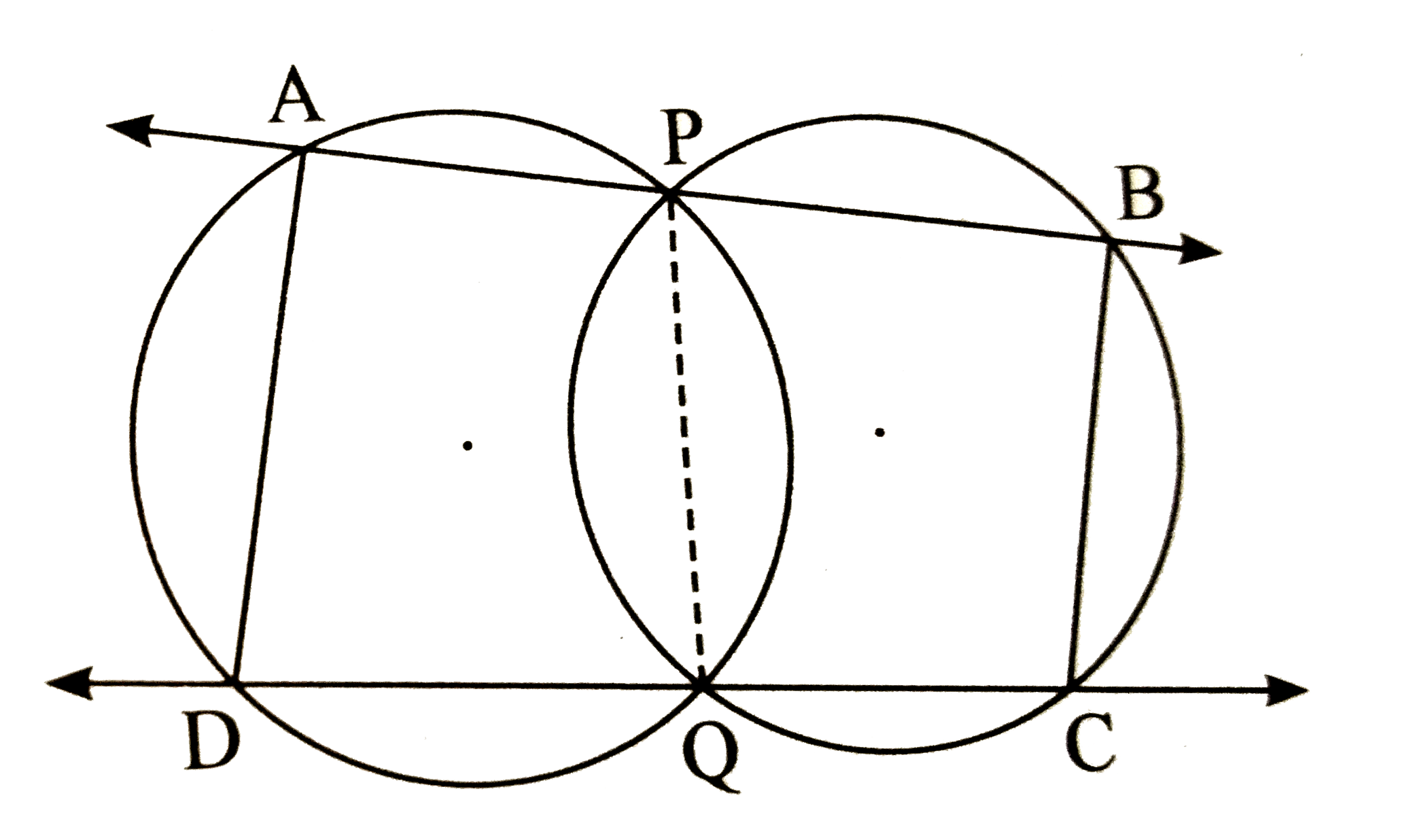
View SolutionTwo circles intersect each other at point P and Q. Secants drawn through p and Q intersect the circles at points A,B and D,C
Prove that :∠ADC+∠BCD=180∘
 View Solution
View Solution

