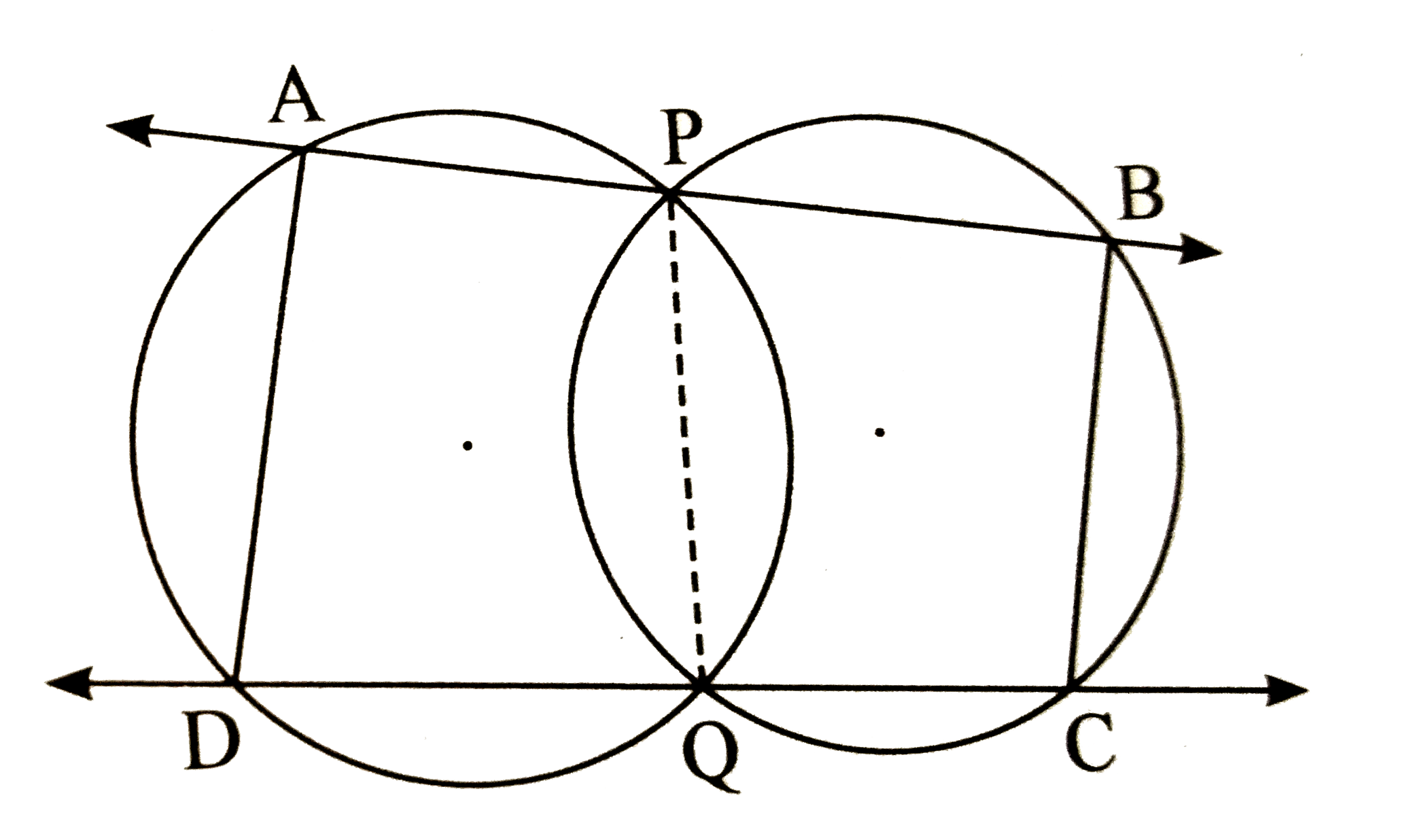
Two equal circles intersect in P and Q. A straight line through P meets the circles inA and B. Prove that QA = QB
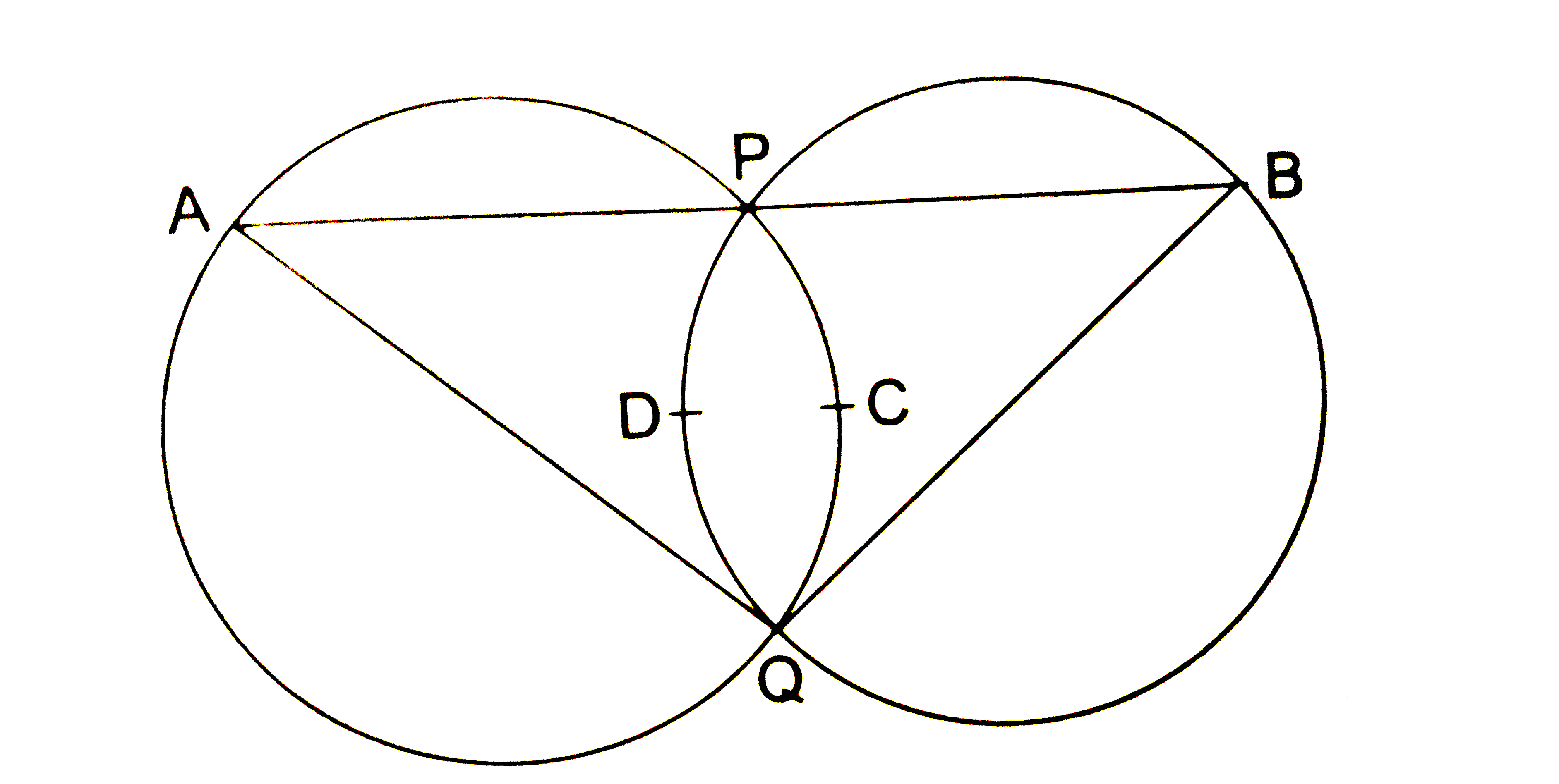
Join PQ.Now, PQ is a common chords of congrent circles. So, arc PCQ = arc PDQ
∴∠QAP=∠QBP⇒QA=QB
Similar Questions
Two equal circles intersect in P and Q . A straight line through P meets the circles in A and B . Prove that QA=QB.
View SolutionTwo circles of equal radii cut each other at P and Q, so that the centre of one lies on the other. A straight line through P cuts the circle again at A and B. Prove that ΔQAB is equilateral triangle.
View SolutionTwo circles intersect each other at the points P and Q. Two straight lines through P and Q intersect one circle at the points A and C and the other circle at B and D. Prove the AC|| BD
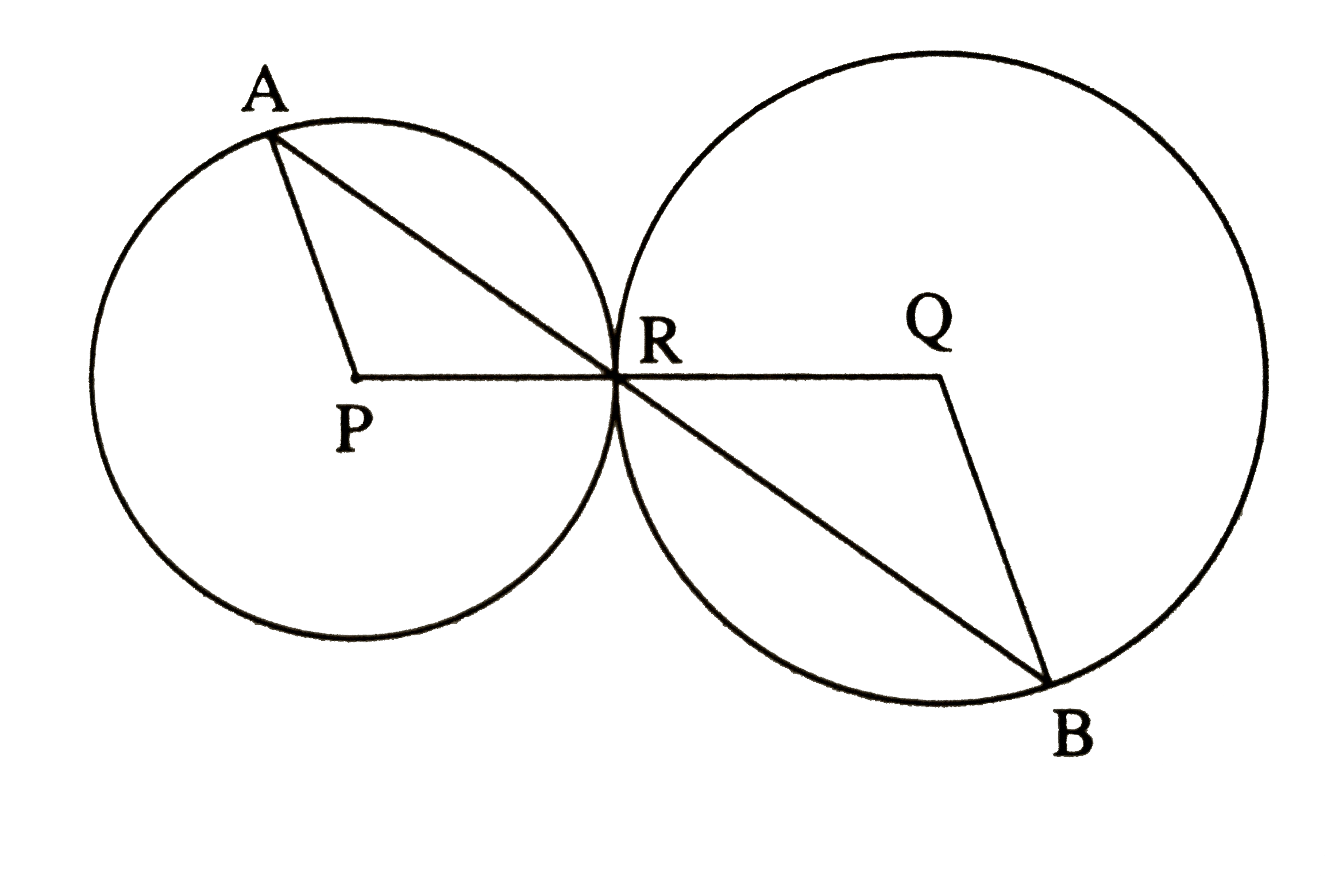
View SolutionIn the figure, the circles with centers P and Q touch each other at R.A line passing through R meets the circles at A and B respectively. Prove that
△APR~△RQB
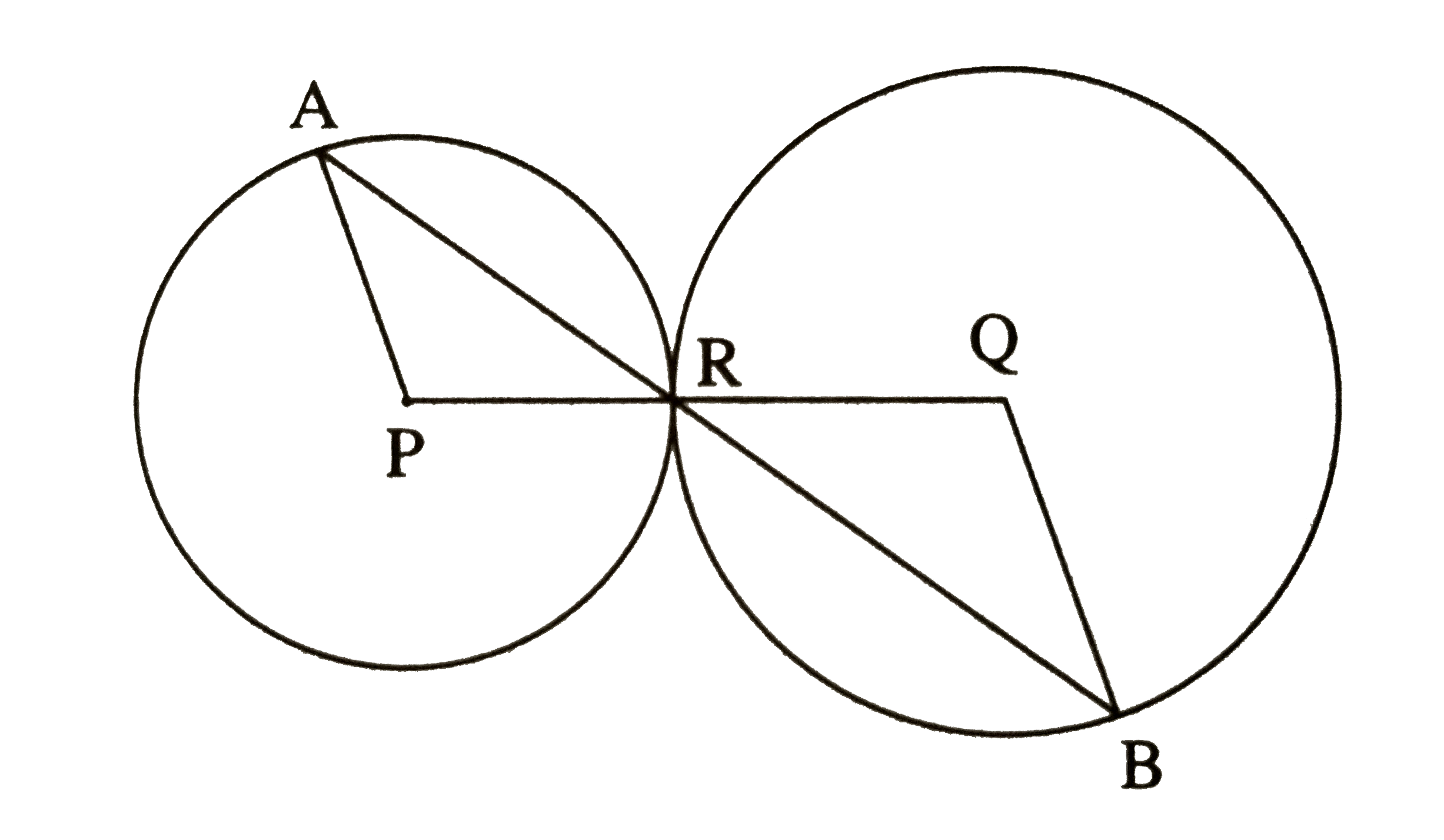
View SolutionIn the figure, the circles with centers P and Q touch each other at R.A line passing through R meets the circles at A and B respectively. Prove that
seg AP || seg BQ
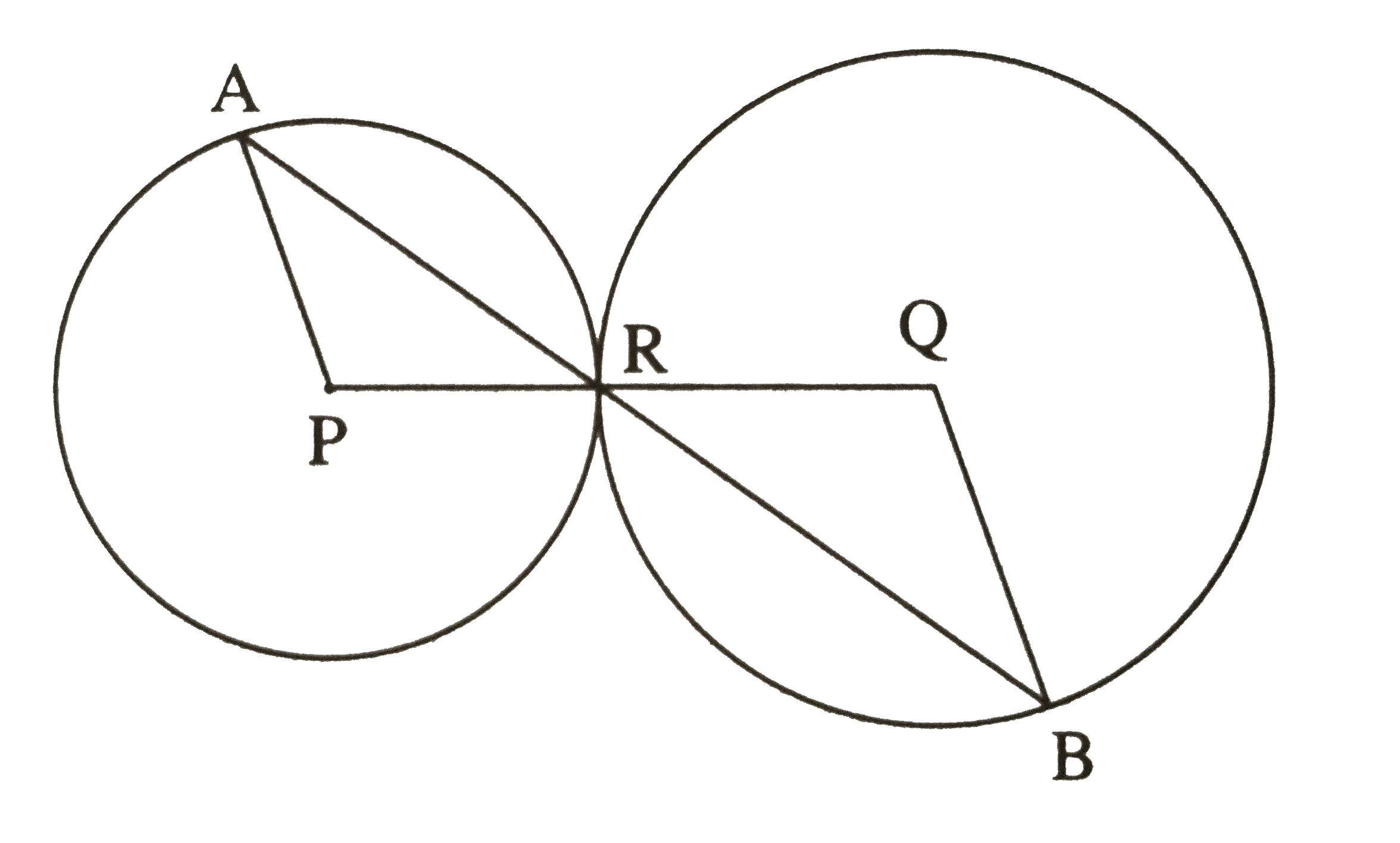
View SolutionIn the figure, the circles with centers P and Q touch each other at R.A line passing through R meets the circles at A and B respectively.
Find ∠RQB if ∠PAR=35∘
View SolutionTwo circles cut at A and B and a straight line PAQ cuts the circles at P and Q. If the tangents at P and Q intersects at R, prove that R,P,B,Q are concyclic.
View SolutionTwo circles intersect each other at point P and Q. Secants drawn through p and Q intersect the circles at points A,B and D,C
Prove that :∠ADC+∠BCD=180∘
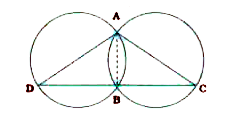
View SolutionIn the figure, two circles intersect each other at points A and B. AP and AQ are the diameters of these circles. Prove that PBQ is a straight line.

View SolutionTwo circles intersect at two points A and B . AD and AC are diameters to the two circles .Prove that B lies on the line segment DC.
View Solution
