Two godowns A and B have gram capacity of 100 quintals and 50 quintals respectively. They supply to 3 ration shops, D. E and F whose requirements are 60, 50 and 40 quintals respectively. The cost of transportation per quintal from the godowns to the shops are given in the following table:How should the supplies be transported in order that the transportation cost is minimum? What is the minimum cost?
Solution :
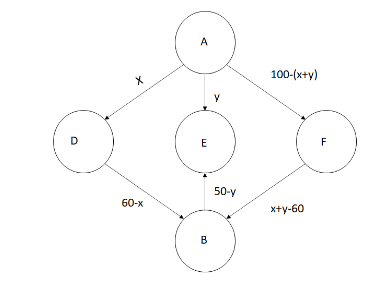
Let godown A supply x and y quintals of grain to the shops D and E respectively. Then, (100−x−y) will be supplied to shop F.
The requirement at shop D is 60 quintals since x quintals are transported from godown A.
Hence, the remaining (60−x) quintals will be transported from godown B. Similarly, (50−y) quintals and 40−(100−x−y)=(x+y−60) quintals will be transported from godown B to shop E and F respectively. The given problem can be represented diagrammatically as follows.
Total transportation cost z is given by,
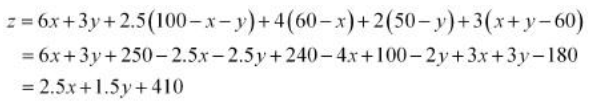
The given problem can be formulated as Minimize z=2.5x+1.5y+410 … (1) subject to the constraints,
x+y≤100...(2)
x≤60...(3)
y≤50...(4)
x+y≥60...(5)
x,y≥0...(6)
The feasible region determined by the system of constraints is as follows.
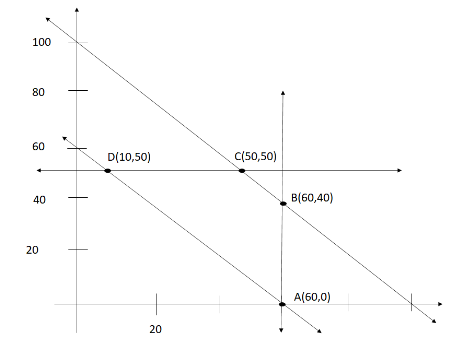
The corner points are A (60,0), B (60,40), C (50,50), and D (10,50). The values of z at these corner points are as follows.
Corner point->2.5x+2.5y+410,
A (60,0) -> 560
B (60,40) ->620
C (50,50) ->610
D (10,50) ->510
The minimum cost of transportation is Rs.510.
Therefore, the amount of grain transported from A to D, E, and F is 10 quintals, 50 quintals, and 40 quintals respectively and from B to D, E, and F is 50 quintals, 0 quintals, and 0 quintals respectively.
Topper's Solved these Questions
- BOOK - NCERT ENGLISHCHAPTER - LINEAR PROGRAMMINGEXERCISE - SOLVED EXAMPLES11videos
LINEAR PROGRAMMING
- BOOK - NCERT ENGLISHCHAPTER - LINEAR PROGRAMMINGEXERCISE - EXERCISE 12.211videos
LINEAR PROGRAMMING
- BOOK - NCERT ENGLISHCHAPTER - LINEAR PROGRAMMINGEXERCISE - EXERCISE 12.211videos
LINEAR PROGRAMMING
- BOOK - NCERT ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Solved Examples13videos
INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - NCERT ENGLISHCHAPTER - MATRICESEXERCISE - All Questions105videos
MATRICES
Similar Questions
Two godowns A and B have grain capacity of 100 quintal and 50 quintal respectively. They supply to 3 ration shops, D, E and F, whose requirements are 60, 50 and 40 quintals respectively. The cost of transportation per quintal from the godowns to the shops are given in the following table:

How should the supplies be transpored in order that the transportation cost is minimum cost?View SolutionTwo godowns A and B have grain capacity of 100 quintals and 50 qunitals respectively. They supply to 3 ration shops, D,E and F whose requirements are 60,50 and 40 quintals repectively.The cost of transportation per quintal from the godowns to the shops are given in the following table:
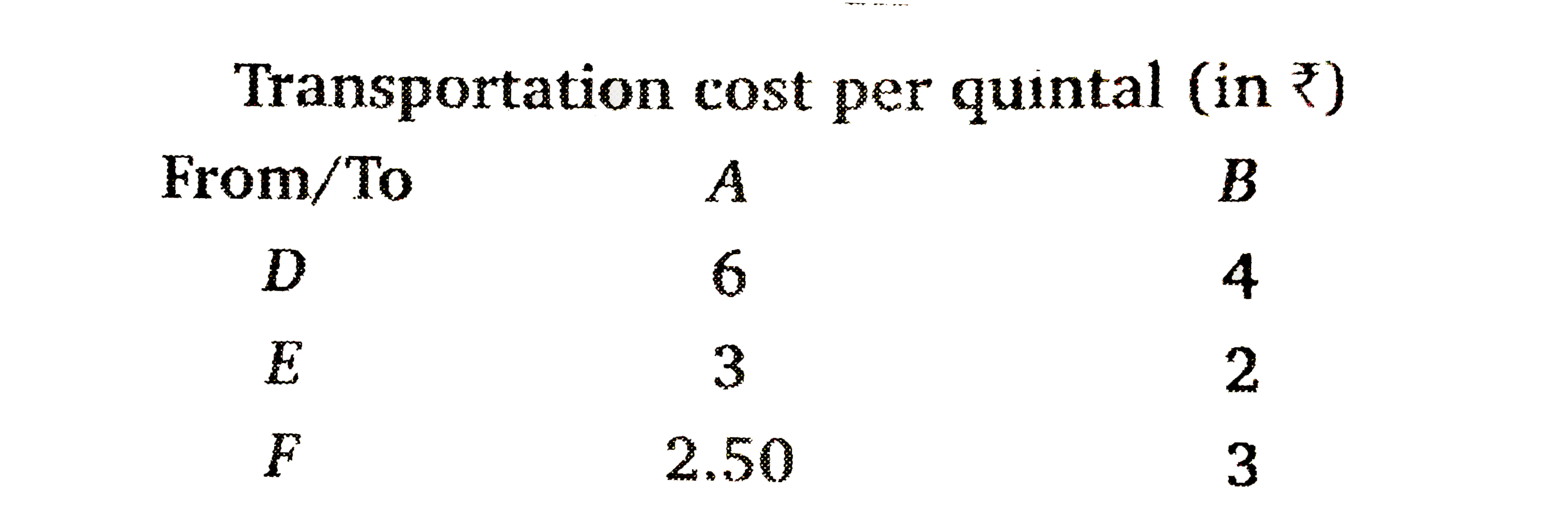
How should the supplies be transported in order that the transportation cost is minimum? What is the minimum cost?View Solution
Knowledge Check
- Question 1 - Select One
1 quintal is equal to
A110 kgB10 kgC100 kgD1000 kg
Two godowns A and B have grain capacity of 100 quintals and 50 qunitals respectively. They supply to 3 ration shops, D,E and F whose requirements are 60,50 and 40 quintals repectively.The cost of transportation per quintal from the godowns to the shops are given in the following table:
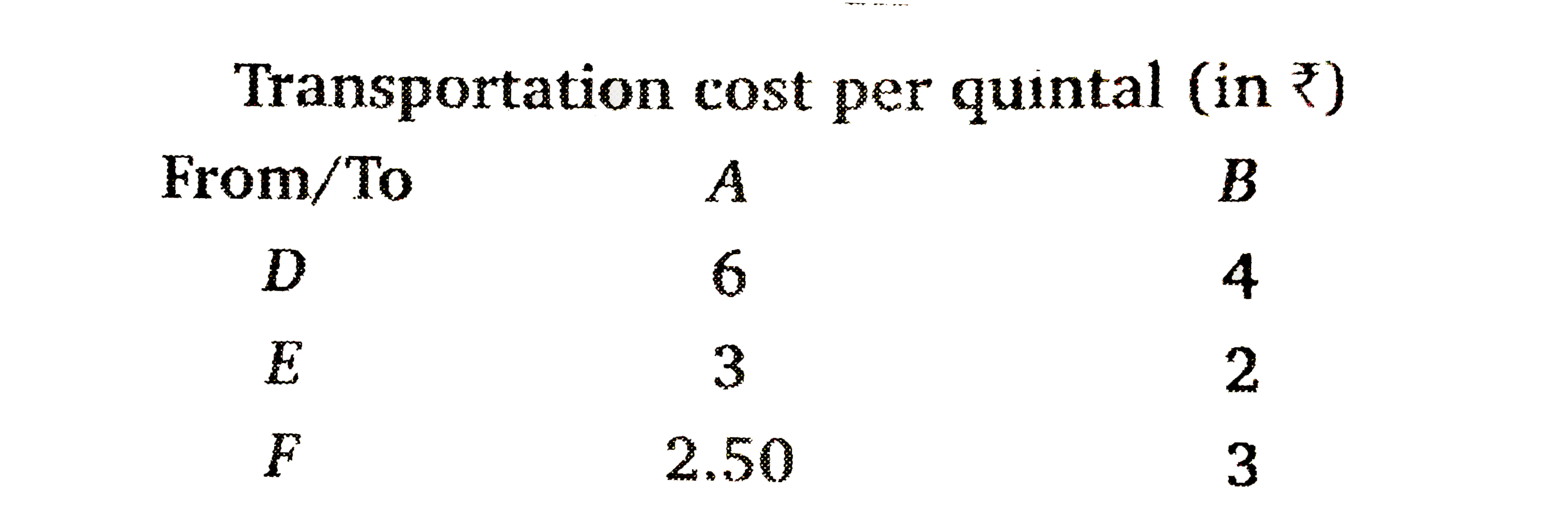
How should the supplies be transported in order that the transportation cost is minimum? What is the minimum cost?View Solution1quintal = ?
View SolutionAn oil company has two depots A and B with capacities of 7000 L and 4000 L respectively. The company is to supply oil to three petrol pumps, D, E and F whose requirements are 4500L, 3000L and 3500L respectively. The distances (in km) between the depots and the petrol pumps is given in the following table:
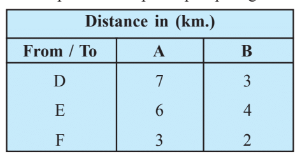
Assuming that the transportation cost of 10 litres of oil is Re 1 per km, how should the delivery be scheduled in order that the transportation cost is minimum? What is the minimum cost?View SolutionAn oil company has two depots A and B with capacities of 7000L and 4000L respectively. The company is to supply oil to three petrol pumps, D,E and F whose requirements are 4500L,3000L and 3500L respectively. The distances (in km) between the depots and the petrol pumpa is given in the following table:

Assuming that the transportation cost of 10 litres of oil is Rs. 1 per km, how shold the delivery be scheduled in order that the transportation cost is minimum? What is the minimum cost?View SolutionAn oil company has two depots, A and B, with capacities of 7000 L and 4000 L respectively. The company is to supply oil to three pumps D,E,F whose requirements are 4500 L, 3000 L and 3500 L respectively. The distance (in Km) between the depots and the petrol pumps are given in the following table :
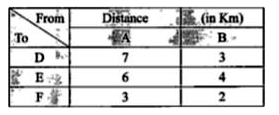
Assuming that the transportation cost of10 litres of oil is ₹ 1 per km , how should the delivery be scheduled in order that the transportation cost is minimum ?View SolutionA medical company has factories at two places, A and B.From these places, supply is made to each of its three agencies situated at P,Q, and R.The monthly requirements of the agencies are respectively 40,40 and 50 packets of the medicines, while the production capacity of the factories A and B, are 60 and 60 packets respectively.The transportation cost per packet from the factories to the agencies are given below:

How many packets from each factory be transported to each agency so that the cost of transportation is minimum? Also find the minimum cost.View Solution(Transportation problem) There are two factories located one at place P and the other at place Q. From these locations, a certain commodity is to be delivered to each of the three depots situated at A, B and C. The weekly requirements of the depots are respectively 5, 5 and 4 units of the commodity while the production capacity of the factories at P and Q are respectively 8 and 6 units. The cost of transportation per unit is given below :
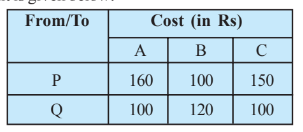
How many units should be transported from each factory to each depot in order that the transportation cost is minimum. What will be the minimum transportation cost?View Solution

