Two hoses attached to separate water sources are available to fill a cyindrical swimming pool. If both hoses are used , the time it will take to fill the pool can be represented by the following equation : 1T1+1T2=1Tc, where T1andT2 represent the time needed for hoses 1 and 2 , respectively , to fill the pool on their own , and Tc represents the time needed for hoses 1 and 2 to fill the pool working together . IF hose 1 alone can fill the pool in exactly 20 minutes and hose 2 alone can fill the pool in exactly 60 minutes , how many minutes will it take to fill the pool if both hoses work simultaneously ?
3
10
15
18
The correct Answer is:C
To solve the problem, we will use the equation provided in the question:
1T1+1T2=1Tc
where:
- T1 is the time taken by hose 1 to fill the pool on its own,
- T2 is the time taken by hose 2 to fill the pool on its own,
- Tc is the time taken by both hoses to fill the pool together.
Step 1: Identify the values of T1 and T2
From the problem, we know:
- Hose 1 can fill the pool in T1=20 minutes.
- Hose 2 can fill the pool in T2=60 minutes.
Step 2: Substitute the values into the equation
Now, we substitute T1 and T2 into the equation:
120+160=1Tc
Step 3: Calculate the left-hand side
To add the fractions 120 and 160, we need a common denominator. The least common multiple (LCM) of 20 and 60 is 60.
Rewriting 120 with a denominator of 60:
120=360
Now we can add:
360+160=460
Step 4: Simplify the fraction
Now simplify 460:
460=115
Step 5: Set the equation for Tc
Now we have:
1Tc=115
Step 6: Solve for Tc
Taking the reciprocal of both sides gives us:
Tc=15
Conclusion
Thus, it will take 15 minutes to fill the pool if both hoses work simultaneously.
---
- T1 is the time taken by hose 1 to fill the pool on its own,
- T2 is the time taken by hose 2 to fill the pool on its own,
- Tc is the time taken by both hoses to fill the pool together.
From the problem, we know:
- Hose 1 can fill the pool in T1=20 minutes.
- Hose 2 can fill the pool in T2=60 minutes.
Now, we substitute T1 and T2 into the equation:
To add the fractions 120 and 160, we need a common denominator. The least common multiple (LCM) of 20 and 60 is 60.
Now simplify 460:
Now we have:
Taking the reciprocal of both sides gives us:
Thus, it will take 15 minutes to fill the pool if both hoses work simultaneously.
Topper's Solved these Questions
Similar Questions
Knowledge Check
1(t−2)2=6+1t−2
If p and q represents the solutions of the equations above, what is the value of p×q?A−32B72C94D156
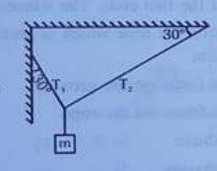
Calculate T1&T2.
View SolutionTwo hoses are pouring water into an empty pool. Hose 1 alone would fill up the pool in 6 hours. Hose 2 alone would fill up the pool in 4 hours. How long would it take for both hoses to fill up two - thirds of the pool?
View SolutionA rectangular swimming pool has a length of 30 meters, a width of 10 meters, and an average depth of 2 meters. If a hose can fill the pool at a rate of 0.5 cubic meters per minute, how many hours will it take the hose to fill the pool?
View SolutionThe focus of the conic represented parametrically by the equation y=t2+3,x=2t−1is
View Solution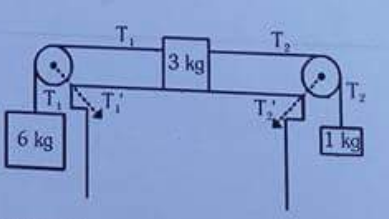
Calculate a, T1,T2,T1'&T2'.
View SolutionThe breakdown of sample of chemical compound is represented by the function p(t)=300(12)t, where p(t) represents the number of milligrams of the substance, and t represents the time , in years. If t=0 represents the year 2015, what will be the first year in which the amount of the substance remaining falls to cless than 5 milligrams?
View SolutionLet r1(t)=3tˆi+4t2ˆj
and r2(t)=4t2ˆi+3tˆj
represent the positions of particles 1 and 2, respectively, as function of time t, r1(t) and r2(t) are in meter and t in second. The relative speed of the two particle at the instant t = 1s, will be
View Solution