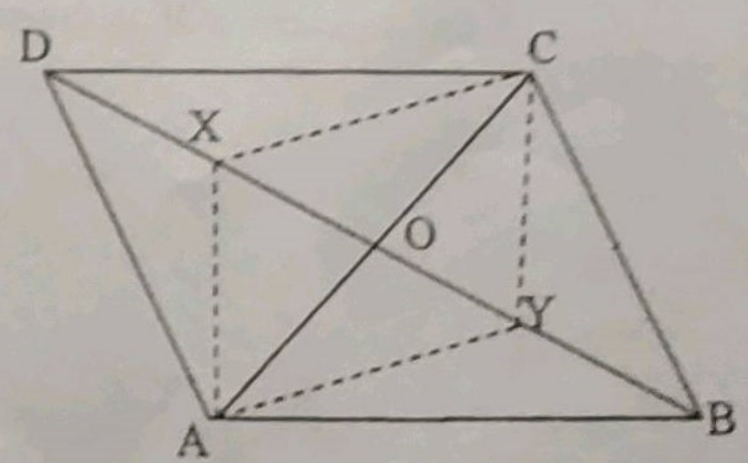
Two points X and Y lie on the diagonal BD of a parallelogram ABCD such that DX = BT. Prove that □AXCY is a parallelogram.
Step by step video, text & image solution for Two points X and Y lie on the diagonal BD of a parallelogram ABCD such that DX = BT. Prove that squareAXCY is a parallelogram. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUADRILATERALSBOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Exercise 8b
15 Videos
- QUADRILATERALSBOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Revision Exercise (very Short Answer Questions)
10 Videos
- QUADRILATERALSBOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Problems From NCERT/exemplar
11 Videos
- PROBABILITYBOOK - NAGEEN PRAKASHANCHAPTER - PROBABILITYEXERCISE - Revision Exercise (very Short Answer /short Answer Questions)
10 Videos
- STATISTICSBOOK - NAGEEN PRAKASHANCHAPTER - STATISTICSEXERCISE - Revision Exercise
10 Videos
Similar Questions
E and F are points on diagonal AC of a parallelogram ABCD such that AE=CF. Show that BFDE is a parallelogram.
View SolutionPoint E and F lie on diagonals AC of a parallelogram ABCD such that AnE=CF. What type of quadrilateral is BFDE? From the given figure we see that BFDEis also a parallelogram.
View Solution
Knowledge Check
X and Y are the mid-points of the opposite sides AB and DC of a parallelogram ABCD. Then □AXCY is a ?
ATrapeziumBKiteCRhombusDParallelogram
In Figure, ABCD is a parallelogram and X and Y are points on the diagonal BD such that DX=BY . Prove that AXCY is a parallelogram (ii) AX=CY, AY=CX AYB ≅CXD (iv) AXD≅ CYB
View SolutionTwo segments AC and BD bisect each other at O . Prove that ABCD is a parallelogram.
View SolutionP is any point on the diagonal BD of the parallelogram ABCD. Prove that ar(△APD) = ar(△CPD).
View SolutionABCD and APCR are the two parallelograms and AC is the common diagonal. Prove that PBRD is a parallelogram.
View SolutionO' is any point on diagonal AC of a parallelogram ABCD. Prove that :
area of ΔAOD= area of ΔAOB
View SolutionIf AM and CN are perpendiculars on the diagonal BD of a parallelogram ABCD, Is ΔAMD≅ΔCNB? Give reason.
View SolutionIf the two diagonals of a parallelogram are equal, it is a rectangle.
View Solution
