P is any point on the diagonal BD of the parallelogram ABCD. Prove that ar(△APD) = ar(△CPD).
Step by step video, text & image solution for P is any point on the diagonal BD of the parallelogram ABCD. Prove that ar(triangleAPD) = ar(triangleCPD). by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - NCERT SECTION ( EXERCISE 9.1)
1 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - NCERT SECTION ( EXERCISE 9.2)
7 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Olympiad/HOTS Corner
14 Videos
- CIRCLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CIRCLES EXERCISE - OLYMPIAD/HOTS CORNER
6 Videos
Similar Questions
In the figure, P is a point in the interior of a parallelogram ABCD. Show that
(i) ar(△APB)+ar(△PCD=12ar(ABCD)
(ii) ar(△APD)+ar(△PBC)=ar(△APB)+ar(△PCD)

View SolutionO is any point on the diagonal PR of a parallelogram PQRS (figure). Prove that ar(ΔPSO)=ar(ΔPQO).

View SolutionO is the any point on diagonal PR of parallelogram PQRS. Prove that Ar(PSO) = Ar(PQO)
View SolutionO' is any point on diagonal AC of a parallelogram ABCD. Prove that :
area of ΔAOD= area of ΔAOB
View SolutionIf P is any point in the interior of a parallelogram ABCD , then prove that area of the triangle APB is less than half the are of parallelogram.
View SolutionTwo points X and Y lie on the diagonal BD of a parallelogram ABCD such that DX = BT. Prove that □AXCY is a parallelogram.
View SolutionIn the adjoining figure, P is the point in the interior of a parallelogram ABCD.Show that ar(DeltaAPB) ar(DeltaPCD) =1/2ar(||gm ABCD)
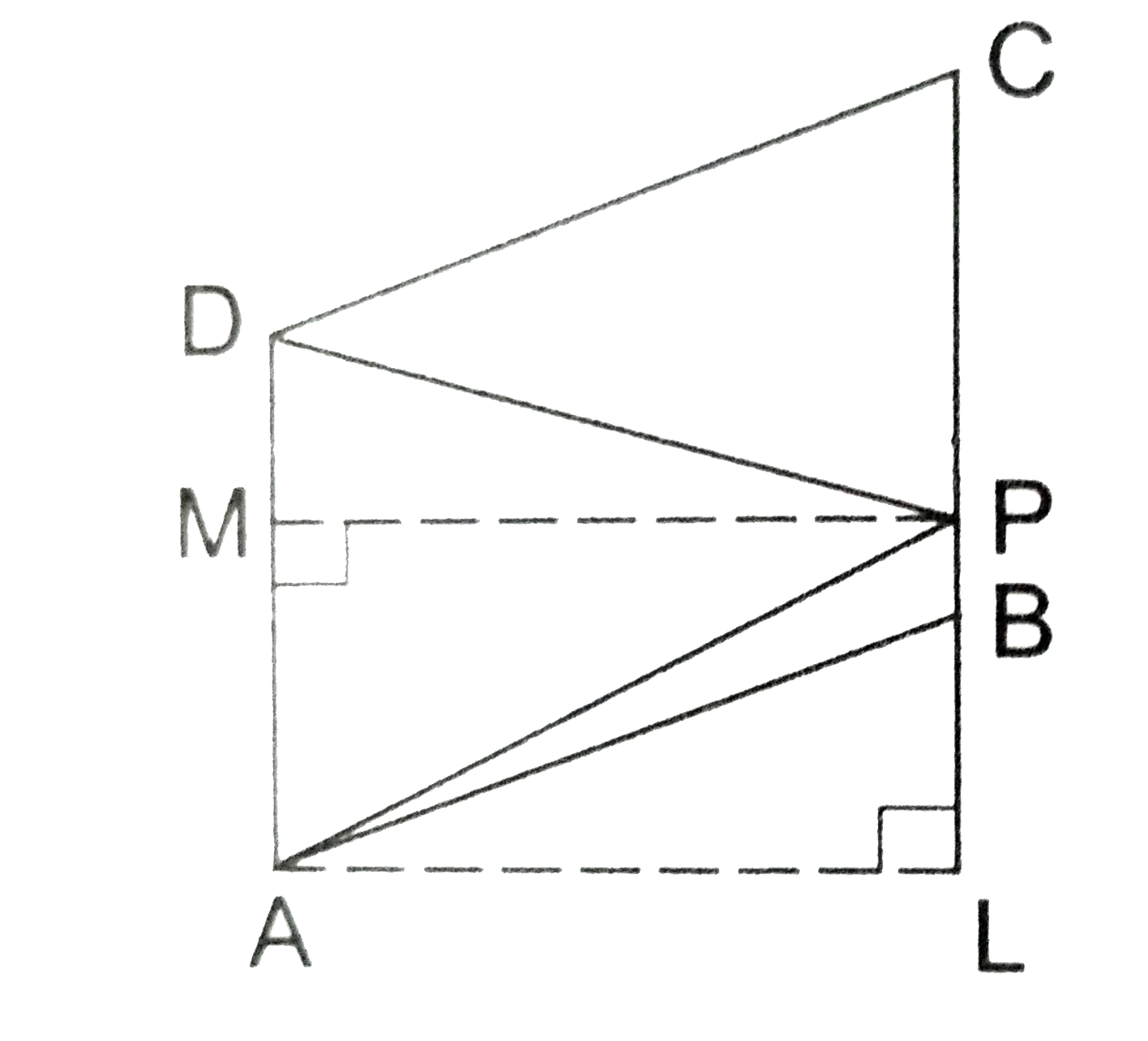
View SolutionIn the adjoining figure, ABCD is a parallelogram and P is any points on BC. Prove that
ar(△ABP)+ar(△DPC)=ar(△PDA).
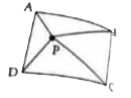
View SolutionIn the adjacent figure P is a point inside the parallelogram ABCD. Prove that
ar (APB) + ar (PCD) = 12 ar (ABCD)
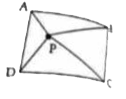
View SolutionIn the adjacent figure P is a point inside the parallelogram ABCD. Prove that
ar (APD) + ar (PBC) = ar (APB) + ar (PCD)
View Solution
