ABCD and APCR are the two parallelograms and AC is the common diagonal. Prove that PBRD is a parallelogram.
To prove that PBRD is a parallelogram given that ABCD and APCR are two parallelograms with AC as a common diagonal, we can follow these steps:
Step 1: Understand the properties of parallelograms
In a parallelogram, opposite sides are equal and parallel. Therefore, for parallelogram ABCD:
- AB = CD (1)
- AD = BC (2)
And for parallelogram APCR:
- AP = CR (3)
- AC = PR (4)
Step 2: Establish relationships between the sides
From the properties of parallelograms, we know:
- AB is parallel to CD (from property (1))
- AD is parallel to BC (from property (2))
- AP is parallel to CR (from property (3))
- AC is parallel to PR (from property (4))
Step 3: Analyze triangles APB and CRD
We will now consider triangles APB and CRD:
- In triangle APB, we have:
- AP = CR (from property (3))
- AB = CD (from property (1))
Step 4: Use the congruence of triangles
Since we have two pairs of equal sides (AP = CR and AB = CD), we can apply the Side-Side-Side (SSS) congruence criterion:
- Triangle APB is congruent to triangle CRD.
Step 5: Establish equal angles
From the congruence of triangles APB and CRD, we can conclude:
- Angle BAP = Angle DCR (corresponding angles of congruent triangles).
Step 6: Show that PB is parallel to DR
Since we have established that:
- AB is parallel to CD (from property (1))
- Angle BAP = Angle DCR,
We can conclude that:
- PB is parallel to DR (by the Alternate Interior Angles Theorem).
Step 7: Show that PBRD is a parallelogram
Now, we need to show that the opposite sides PB and DR are equal and parallel:
- PB = DR (from the congruence of triangles APB and CRD).
- PB is parallel to DR (from the previous step).
Conclusion
Since both pairs of opposite sides (PB and DR) are equal and parallel, we can conclude that PBRD is a parallelogram.
In a parallelogram, opposite sides are equal and parallel. Therefore, for parallelogram ABCD:
- AB = CD (1)
- AD = BC (2)
And for parallelogram APCR:
- AP = CR (3)
- AC = PR (4)
From the properties of parallelograms, we know:
- AB is parallel to CD (from property (1))
- AD is parallel to BC (from property (2))
- AP is parallel to CR (from property (3))
- AC is parallel to PR (from property (4))
We will now consider triangles APB and CRD:
- In triangle APB, we have:
- AP = CR (from property (3))
- AB = CD (from property (1))
Step 4: Use the congruence of triangles
Since we have two pairs of equal sides (AP = CR and AB = CD), we can apply the Side-Side-Side (SSS) congruence criterion:
- Triangle APB is congruent to triangle CRD.
From the congruence of triangles APB and CRD, we can conclude:
- Angle BAP = Angle DCR (corresponding angles of congruent triangles).
Since we have established that:
- AB is parallel to CD (from property (1))
- Angle BAP = Angle DCR,
We can conclude that:
- PB is parallel to DR (by the Alternate Interior Angles Theorem).
Now, we need to show that the opposite sides PB and DR are equal and parallel:
- PB = DR (from the congruence of triangles APB and CRD).
- PB is parallel to DR (from the previous step).
Since both pairs of opposite sides (PB and DR) are equal and parallel, we can conclude that PBRD is a parallelogram.
Topper's Solved these Questions
- QUADRILATERALS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - QUADRILATERALS EXERCISE - EXERCISE (Integer/Numerical Value Type)
10 Videos
- QUADRILATERALS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - QUADRILATERALS EXERCISE - Olympiad/HOTS CORNER
15 Videos
- QUADRILATERALS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - QUADRILATERALS EXERCISE - EXERCISE (Subjective Problems) (Short Answer Type)
5 Videos
- PROBABILITYBOOK - MTG IIT JEE FOUNDATIONCHAPTER - PROBABILITYEXERCISE - OLYMPIAD/HOTS CORNER
20 Videos
- STATISTICSBOOK - MTG IIT JEE FOUNDATIONCHAPTER - STATISTICSEXERCISE - Olympiad/HOTS Corner
20 Videos
Similar Questions
In the figure ABCD and DXBY are two parallelograms with BD as the common diagonal. Prove that AYCX is also a parallelogram.
View SolutionThe sides AB and CD of a parallelogram ABCD are bisected at EandF . Prove that EBFD is a parallelogram.
View SolutionTwo segments AC and BD bisect each other at O . Prove that ABCD is a parallelogram.
View SolutionABCD and APQR are two parallelograms. Prove that ∠C=∠Qand∠B=∠R
View SolutionE and F are points on diagonal AC of a parallelogram ABCD such that AE=CF. Show that BFDE is a parallelogram.
View SolutionIn a parallelogram ABCD, points P and Q are points of trisection of diagonal BD. Prove that CQ is parallel to AP.
View SolutionIn parallelogram ABCD, E is the mid-point of AD and F is the mid-point of BC. Prove that BFDE is a parallelogram.
View SolutionIn the adjoining figure, prove that ABCD is a parallelogram. Also find its area.
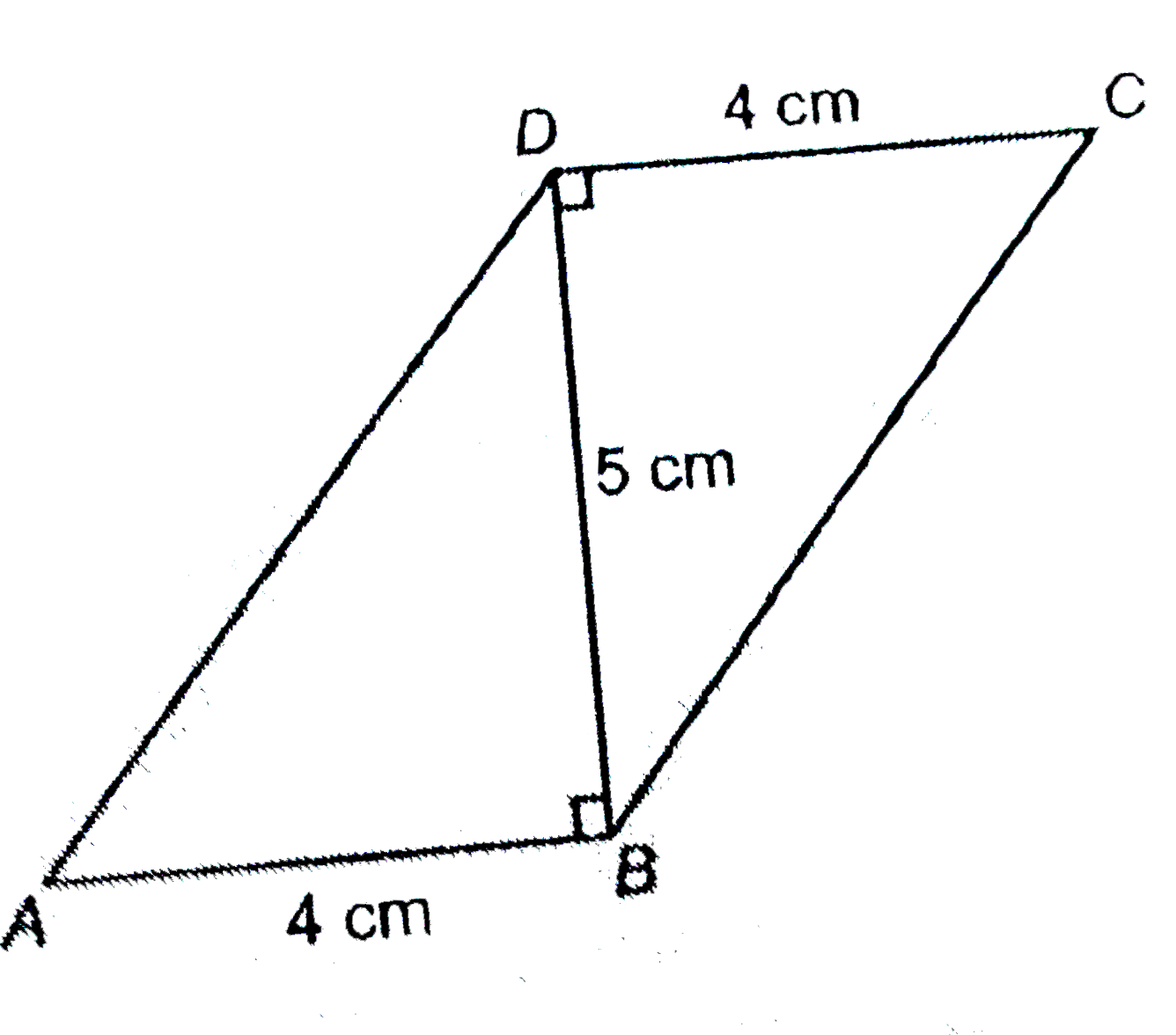
View SolutionTwo points X and Y lie on the diagonal BD of a parallelogram ABCD such that DX = BT. Prove that □AXCY is a parallelogram.
View SolutionABCD is a quadrilateral and BD is one of its diagonals as shown in Figure. Show that ABCD is a parallelogram and find its area.
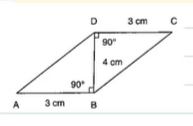
View Solution
