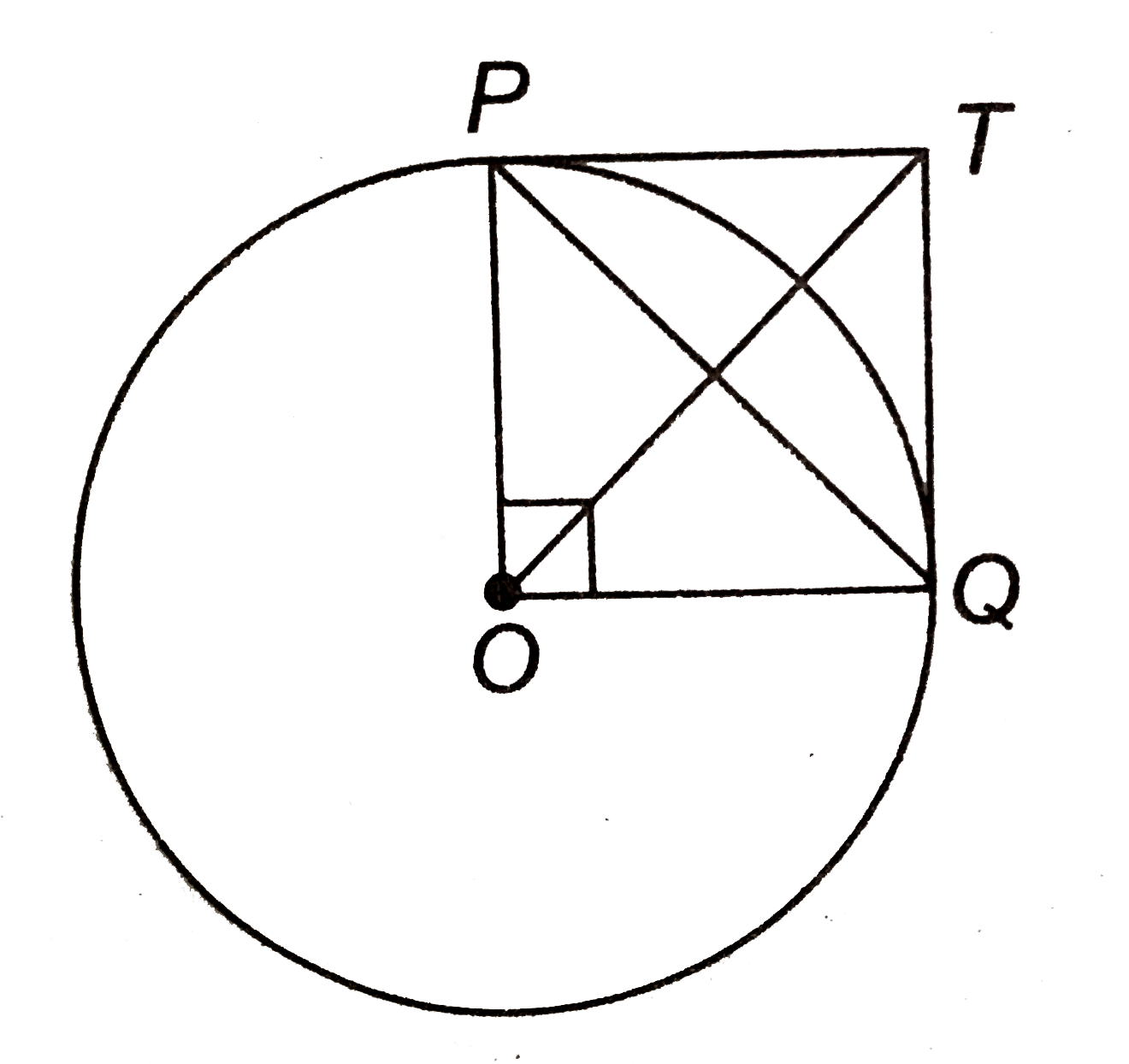
Two radii OA and OB of a circle with centre O are perpendicular to each other. If two tangents are drawn at the point A and B intersect each other at the point T, prove that AB=OT and they bisect each other at a ridght angle. Solution in Bengali
Two radii OA and OB of a circle with centre at O are prependicular to ecah other. Two tangents ST and RT at the points A and B respectively intersect each other at T.
Let us join the points A, B and O, T. Let AB and OT intersect eacth other at C.
To prove : AB=OT and AB and OT bisect each other at a right angle.
Proof : In the quadrilateral OATB,OA⊥OB (given),∴∠AOB=90∘,OA⊥TS,∠OAT=90∘andOB⊥TR∴∠OBT=90∘,i.e., three of the angles of OATB are right-angles. So, the fourth angle is also a right angle.
∴ each of the angles of OATB is a right angle.
Again, OA=OB[∵ radii of same circle]
∴OA=OB=BT=TA.
therefoer each of the side of the quadrillateral OATB are eqial and each of the angles is a right angle.

∴OATB is a square and AB and OT are two of its diagonals.
We know that diagonals of a square are equal and the diagonals bisect each other at right-angles.
∴AB=OT and AB and OT bisect each other at a right angle. [Proved]
Topper's Solved these Questions
- THEOREMS RELATED TO TANGENT IN A CIRCLE BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO TANGENT IN A CIRCLE EXERCISE - EXERCISE 4.1
20 Videos
- THEOREMS RELATED TO TANGENT IN A CIRCLE BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO TANGENT IN A CIRCLE EXERCISE - EXERCISE 4.2
23 Videos
- THEOREMS RELATED TO ANGLES IN A CIRCLEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXERCISE 2.3 (Long Answer Type Questions)
14 Videos
- TRIGONOMETRIC RATIOS AND TRIGONOMETRIC IDENTITIES BOOK - CALCUTTA BOOK HOUSECHAPTER - TRIGONOMETRIC RATIOS AND TRIGONOMETRIC IDENTITIES EXERCISE - EXERCISE
66 Videos
Similar Questions
PR and PS are two tangents drawn from a extental point P of the Circle with centre at O. If PR=8cmand∠RPO=60∘, then the length of PS=
View SolutionThe distance of the point from the centre of a circle with diameter of 16 cm is 17 cm. Then the length of the tangent from the point to the circle is
View SolutionProve that angle in the segment of a circle which is greater than a semi-circle is an acute angle.
View SolutionIf tanθ=pq, what is the value of psecθ−q cosecθpsecθ+q cosecθ=
View SolutionThe radius of a circle with centre O is 7 cm. Two radii OA and OB are drawn at right angles to each other. Find the areas of minor and major segments.
View Solutionचित्र में O एवं O' केन्द्र के दो वृत्त एक-दूसरे का बाह्यतः बिन्दु C पर स्पर्श करते है। इन वृत्तों की एक उभयनिष्ठ स्पर्श रेखा AB खींची गई है। सिद्ध कीजिए कि ∠ACB=90∘
View Solutionदो वृत्तों के केन्द्र O और O ' है, जो एक-दूसरे को बाहृतः बिन्दु P पर स्पर्श करते है। इन वृत्तों की एक उभयनिष्ट अनुस्पर्श रेखा AB खींची जाती है। सिद्ध कीजिए कि ∠APB=90∘.
View Solutionदो वृत्त एक-दूसरे को दो बिन्दुओं पर प्रतिच्छेद करते हैं | सिद्ध कीजिए कि इनके केन्द्रों को मिलाने वाली रेखा, उभयनिष्ठ जीवा को लम्ब समद्विभाजित करती है |
View SolutionTwo chords AB and CD of a circle with centre O intersect each other at the point P. prove that AOD+∠BOC=2∠PBC. If ∠BOC are supplementary to each other, then prove that the two chords are perpendicular to each other.
View SolutionTwo chords AC and BD of a circle intersect each other at the point O. If two tangents drawn at the points A and B intersect each other at the point P and two tangents drawn at the points C and D intersect at the point Q, prove that ∠P+∠Q=2∠BOC.[GP−X]
View SolutionTwo tangents drawn at the point A and B on a circle intersect each other at the point P. If ∠APB=60∘, then ∠PAB=
View Solutionदी आकृति में, PO⊥QO है। O केन्द्र के वृत्त में, बिन्दु P और Q पर खींची स्पर्श रेखायें बिन्दु T पर कटती है। सिद्ध कीजिए कि PQ और OT एक-दूसरे को समकोण पर समद्विभाजित करती है।
View SolutionTwo simple lines PQ and RS intersect each other at O point. If the line OA, anglePOR Co and line OB, angleQOS If bisects, prove that OA and OB will be located on the same straight line.
View SolutionTwo tangents AB and AC are drawn from an external point A to a circle with centre O . If they are inclined to each other at an angle of 100∘ then what is the value of ∠BOC.
View SolutionO The two chords AB and CD of a central circle intersect at the point P. Prove that angleAOD+angleBOC=2angleBPC . If angleAOD Oh angleBOC If they complement each other, then we prove that the two chords are perpendicular to each other.
View Solution
