Two tangents AB and AC are drawn from an external point A to a circle with centre O . If they are inclined to each other at an angle of then what is the value of
The correct Answer is:
To solve the problem, we will follow these steps:
Step 1: Understand the configuration
We have a circle with center O and two tangents AB and AC drawn from an external point A. The angle between the tangents AB and AC is given as 100°.
Step 2: Identify the angles
Since AB and AC are tangents to the circle, the radius at the point of tangency (let's say points B and C) is perpendicular to the tangent. Therefore, we have:
- Angle OAB = 90°
- Angle OAC = 90°
Step 3: Use the properties of triangles
Since the tangents AB and AC are equal in length (tangents drawn from an external point to a circle are equal), triangles OAB and OAC are congruent. Thus:
- OB = OC (radii of the circle)
- OA is common to both triangles
Step 4: Establish relationships between angles
From the congruence of triangles OAB and OAC, we can say:
- Angle OAB = Angle OAC
Let’s denote Angle OAB as x. Then:
- Angle OAB + Angle OAC + Angle BAC = 100°
- 2x + 100° = 100°
- 2x = 100° - 100°
- 2x = 0°
- x = 50°
Step 5: Find angle BOA
Now, we know:
- Angle OAB = 50°
- Angle OBA = 90° (since it is a right angle)
Using the triangle sum property in triangle OAB:
- Angle OAB + Angle OBA + Angle BOA = 180°
- 50° + 90° + Angle BOA = 180°
- Angle BOA = 180° - 140°
- Angle BOA = 40°
Step 6: Find angle BOC
Since triangles OAB and OAC are congruent, Angle COA is also 40°.
Thus, we can find Angle BOC:
- Angle BOC = Angle BOA + Angle COA
- Angle BOC = 40° + 40°
- Angle BOC = 80°
Final Answer
The value of angle BOC is 80°.
---
We have a circle with center O and two tangents AB and AC drawn from an external point A. The angle between the tangents AB and AC is given as 100°.
Since AB and AC are tangents to the circle, the radius at the point of tangency (let's say points B and C) is perpendicular to the tangent. Therefore, we have:
- Angle OAB = 90°
- Angle OAC = 90°
Since the tangents AB and AC are equal in length (tangents drawn from an external point to a circle are equal), triangles OAB and OAC are congruent. Thus:
- OB = OC (radii of the circle)
- OA is common to both triangles
From the congruence of triangles OAB and OAC, we can say:
- Angle OAB = Angle OAC
- Angle OAB + Angle OAC + Angle BAC = 100°
- 2x + 100° = 100°
- 2x = 100° - 100°
- 2x = 0°
- x = 50°
Now, we know:
- Angle OAB = 50°
- Angle OBA = 90° (since it is a right angle)
- Angle OAB + Angle OBA + Angle BOA = 180°
- 50° + 90° + Angle BOA = 180°
- Angle BOA = 180° - 140°
- Angle BOA = 40°
Since triangles OAB and OAC are congruent, Angle COA is also 40°.
Thus, we can find Angle BOC:
- Angle BOC = Angle BOA + Angle COA
- Angle BOC = 40° + 40°
- Angle BOC = 80°
The value of angle BOC is 80°.
Topper's Solved these Questions
- CIRCLES BOOK - VK GLOBAL PUBLICATIONCHAPTER - CIRCLES EXERCISE - PROFICIENCY EXERCISE (Short Answer Questions - II 3 mark)
22 Videos
- CIRCLES BOOK - VK GLOBAL PUBLICATIONCHAPTER - CIRCLES EXERCISE - PROFICIENCY EXERCISE (Long Answer Questions 4 mark)
12 Videos
- CIRCLES BOOK - VK GLOBAL PUBLICATIONCHAPTER - CIRCLES EXERCISE - PROFICIENCY EXERCISE (Very Short Answer Questions 1 mark)
13 Videos
- ARITHMETIC PROGRESSIONS BOOK - VK GLOBAL PUBLICATIONCHAPTER - ARITHMETIC PROGRESSIONS EXERCISE - SELF ASSESSMENT TEST
10 Videos
- COORDINATE GEOMETRY BOOK - VK GLOBAL PUBLICATIONCHAPTER - COORDINATE GEOMETRY EXERCISE - SELF-ASSESSMENT TEST
10 Videos
Similar Questions
Two tangents TP and TQ are drawn from an external point T to a circle with centre O as shown in figure. If they are inclined to each other at an angle of 100∘, then what is the value of ∠POQ?
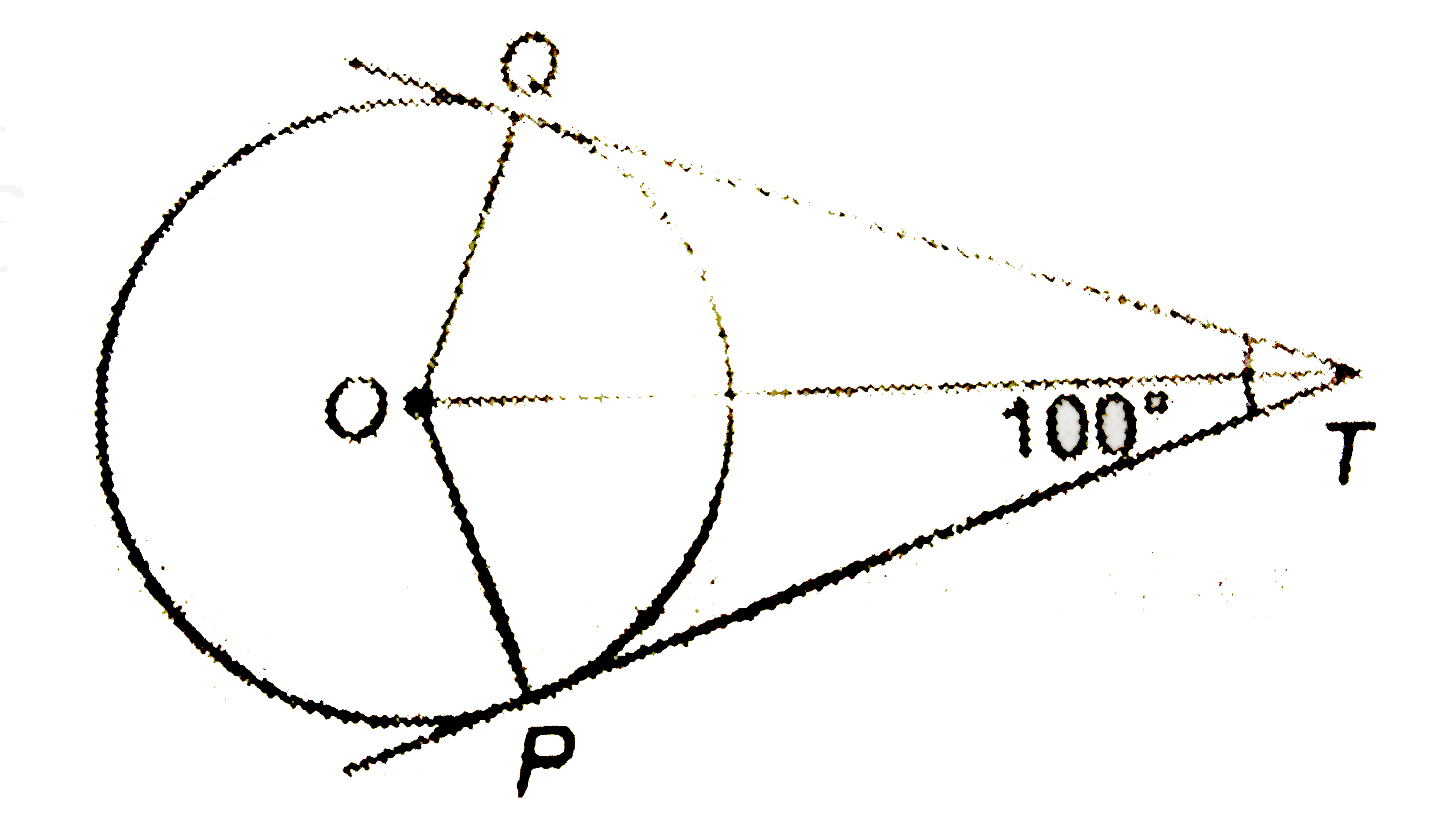
View SolutionTwo tangents TP and TQ are drawn from an external point T to a circle with centre O as shown in Fig. 10.73. If they are inclined to each other at an angle of 100o , then what is the value of ∠POQ ?
View Solution
Knowledge Check
If tangents PA and PB from a point P to a circle with centre O are inclined to each other at an angle of 70∘, then ∠POA is equal to
A70∘B55∘C100∘D40∘If tangent PA and PB from a point P to a circle with centre O are inclined to each other at angle 80∘, then ∠POA is equal to
A50∘B60∘C70∘D80∘
If tangents PA and PB from a point P to a circle with centre O are inclined to each other at an angle of 110∘ , find ∠POA.
View SolutionTwo tangents PQ and PR are drawn from an external point to a circle with centre 0. Prove that QORP is cyclic quadrileral.
View SolutionIf tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of 80∘ , then find ∠POA .
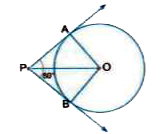
View SolutionIf tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of 80∘, then ∠POA is equal to
View Solutiontwo tangents RQ and RP are drawn from an external point R to the circle with centre O. If ∠PRQ=120∘ , then prove that OR= PR+ RQ
View SolutionIn Fig . pair of tangents AP and AQ drawn from an external point A to a circle with centre O are perpendicular to each other and length of each tangent is 5 cm. Find the radius of the circle.
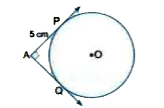
View Solution
