Two runner A and B start at the origin and run along positive x axis ,with B running three times as fast as A. An obsever, standeing one unit above the origin , keeps A and B in view.Then the maximum angle theta of sight between the observer's view of A and B is
π/8
π/6
π/3
π/4
The correct Answer is:2
To solve the problem step by step, we can follow these instructions:
Step 1: Define Variables
Let the speed of runner A be vA. Then, the speed of runner B, who runs three times as fast, will be vB=3vA.
Step 2: Distance Traveled by Runners
At any time t:
- The distance traveled by runner A is x=vAt.
- The distance traveled by runner B is 3x=3vAt.
Step 3: Set Up the Coordinate System
We can represent the positions of the runners in a coordinate system:
- Runner A's position at time t is (x,0).
- Runner B's position at time t is (3x,0).
- The observer is located at point O(0,1).
Step 4: Calculate Angles of Sight
We need to find the angles of sight from the observer to each runner:
- For runner A, the angle θ1:
tan(θ1)=yx=1x
- For runner B, the angle θ2:
tan(θ2)=y3x=13x
Step 5: Find the Angle Between the Lines of Sight
The angle θ between the lines of sight to runners A and B can be expressed as:
tan(θ)=tan(θ2−θ1)=tan(θ2)−tan(θ1)1+tan(θ1)tan(θ2)
Step 6: Substitute the Values
Substituting the values of tan(θ1) and tan(θ2):
tan(θ)=13x−1x1+(1x)(13x)
This simplifies to:
tan(θ)=1−33x1+13x2=−23x1+13x2=−23x+1x
Step 7: Maximize the Angle
To find the maximum value of tan(θ), we need to maximize:
y=−23x+1x
We can differentiate this with respect to x and set the derivative to zero to find critical points.
Step 8: Differentiate and Solve
Differentiating y:
dydx=ddx(−23x+1x)
Using the quotient rule, we find:
dydx=0⋅(3x+1x)−(−2)(3−1x2)(3x+1x)2
Setting the numerator equal to zero gives:
2(3−1x2)=0⟹3=1x2⟹x2=13⟹x=1√3
Step 9: Determine the Maximum Angle
Substituting x=1√3 back into the expression for tan(θ):
tan(θ)=2√33+3=2√36=√33
Thus, the maximum angle θ is:
θ=tan−1(√33)=π6 radians=30∘
Final Answer
The maximum angle θ of sight between the observer's view of A and B is 30∘.
---
Let the speed of runner A be vA. Then, the speed of runner B, who runs three times as fast, will be vB=3vA.
At any time t:
- The distance traveled by runner A is x=vAt.
- The distance traveled by runner B is 3x=3vAt.
We can represent the positions of the runners in a coordinate system:
- Runner A's position at time t is (x,0).
- Runner B's position at time t is (3x,0).
- The observer is located at point O(0,1).
We need to find the angles of sight from the observer to each runner:
- For runner A, the angle θ1:
tan(θ1)=yx=1x
- For runner B, the angle θ2:
tan(θ2)=y3x=13x
The angle θ between the lines of sight to runners A and B can be expressed as:
tan(θ)=tan(θ2−θ1)=tan(θ2)−tan(θ1)1+tan(θ1)tan(θ2)
Substituting the values of tan(θ1) and tan(θ2):
tan(θ)=13x−1x1+(1x)(13x)
This simplifies to:
tan(θ)=1−33x1+13x2=−23x1+13x2=−23x+1x
To find the maximum value of tan(θ), we need to maximize:
y=−23x+1x
We can differentiate this with respect to x and set the derivative to zero to find critical points.
Differentiating y:
dydx=ddx(−23x+1x)
Using the quotient rule, we find:
dydx=0⋅(3x+1x)−(−2)(3−1x2)(3x+1x)2
Setting the numerator equal to zero gives:
2(3−1x2)=0⟹3=1x2⟹x2=13⟹x=1√3
Substituting x=1√3 back into the expression for tan(θ):
tan(θ)=2√33+3=2√36=√33
Thus, the maximum angle θ is:
θ=tan−1(√33)=π6 radians=30∘
The maximum angle θ of sight between the observer's view of A and B is 30∘.
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Multiple correct answers type48videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Numerical Value Type24videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Concept Application Exercise 6.75videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - METHODS OF DIFFERENTIATIONEXERCISE - Single Correct Answer Type46videos
METHODS OF DIFFERENTIATION
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Comprehension Type6videos
MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONS
Similar Questions
Two particles A and B start from the origin along x-axis. Velocity time graph of both particles are shown in the figure. During the given time interval, the maximum separation between the particles is
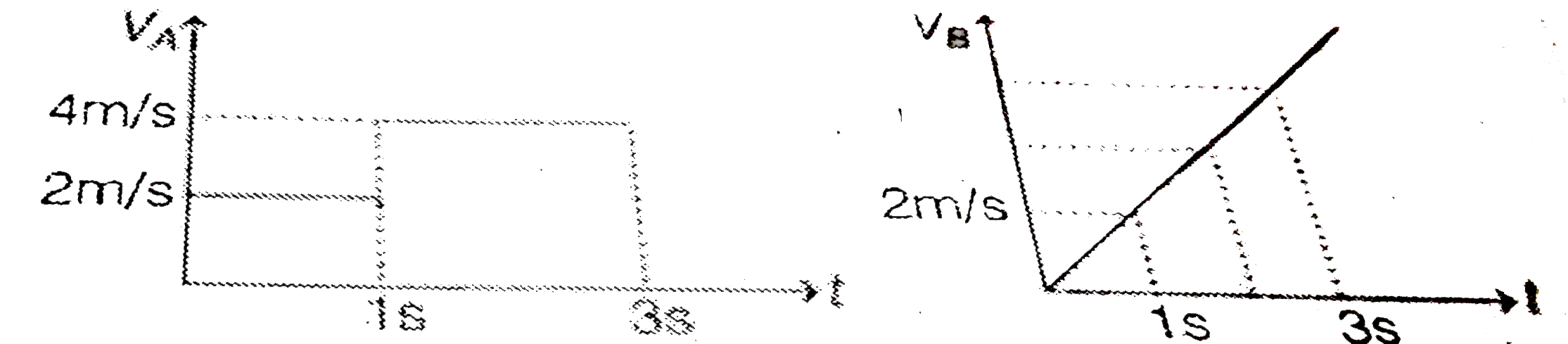 View Solution
View SolutionIn rectangle OABC, point O is the origin, OA=10 units along x-axis and AB=8 units. Find the co-ordinates of vertices A,B and C.
View SolutionTwo persons A and B are standing at the origin and 210 meter away from the origin along the y-axis, respectively. A starts to move along x axis with acceleration 3.2m/s2 and thereafter with the same retardation and comes to rest after moving 320 m B moves with a constant velocity and catches A in 15 s. The speed of B is 10n3m/s. Find the value of n.
View SolutionTwo paricles A and B start at the origin O and travel in opposite directions along the circular path at constant speeds vA=0.7ms−1 and vB=1.0ms−1, respectively.
Determine the time when they collide and the magnitude of the acceleration of B just before this happens.
 View Solution
View SolutionA circle of radius 1 unit touches the positive x-axis and the positive y-axis at A and B , respectively. A variable line passing through the origin intersects the circle at two points D and E . If the area of triangle DEB is maximum when the slope of the line is m, then find the value of m−2
View SolutionA particle is moving with speed v=b√x along positive x-axis. Calculate the speed of the particle at time t=τ (assume tha the particle is at origin at t= 0).
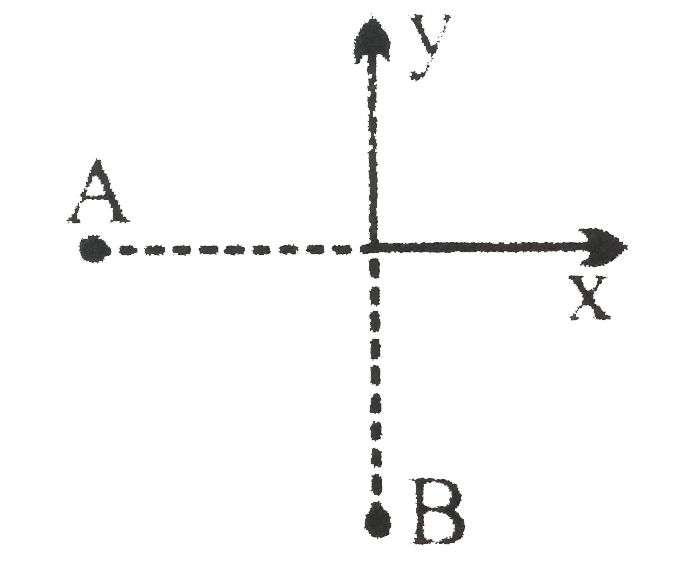
View SolutionTwo bodies A and B are moving along y-axis and x -axis as shown. Find the minimum distance between A and B is subsequent motion (in m)
 View Solution
View SolutionParticles A and B are moving with constant velocities along x and y axis respectively, the graph of separation between them with time is
 View Solution
View SolutionA cube is placed so that one corner is at the origin and three edges are along the x-,y-, and ,z-axes of a coordinate system (figure).Use vector to compute
a.The angle between the edge along the z-axis (line ab) and the diagonal from the origin to the opposite corner (line ad).
b. The angle between line ac (the diagonal of a face ) and line ad.
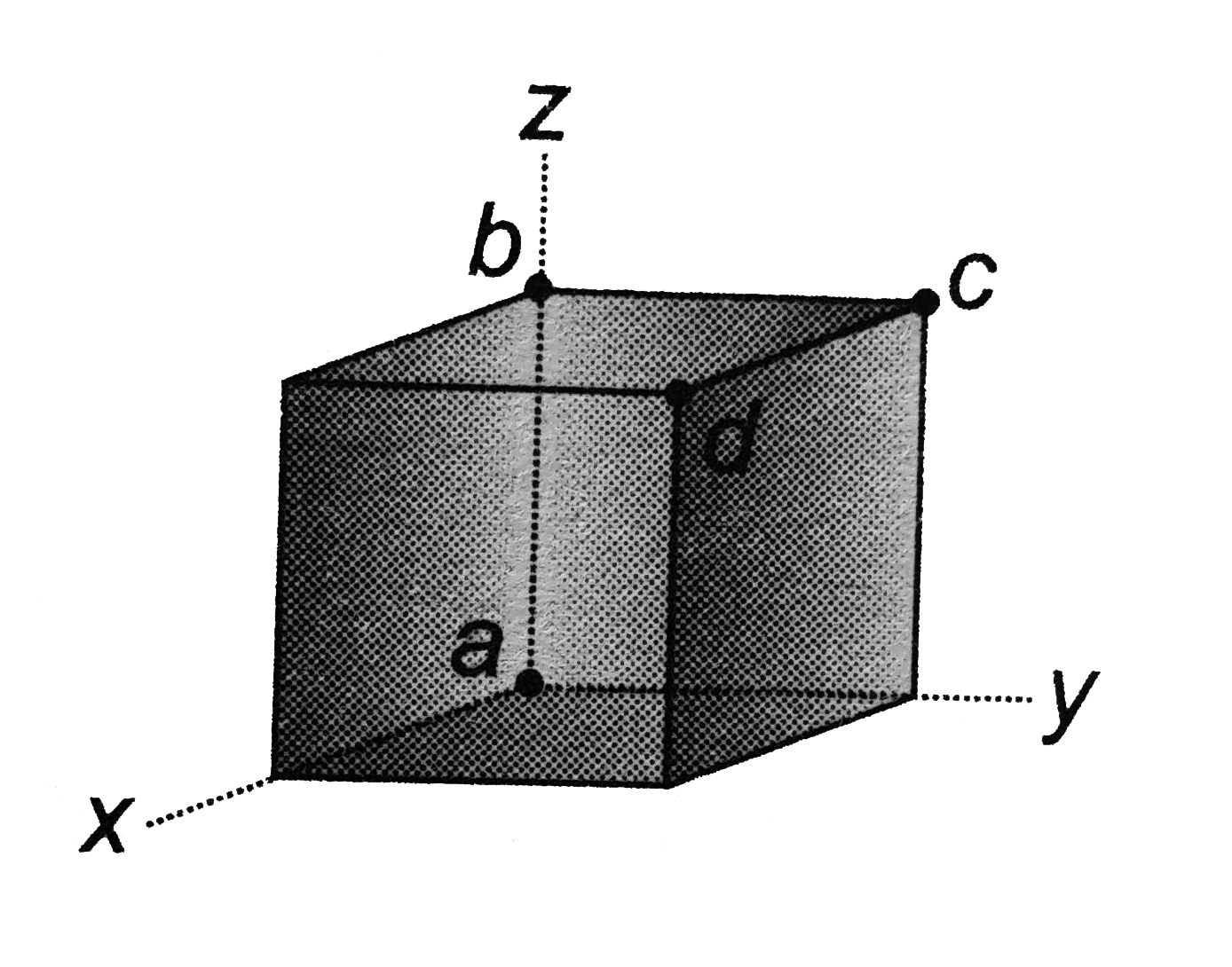 View Solution
View SolutionIf →a and →b are two unit vectors and θ is the angle between them, then the unit vector along the angular bisector of →a and →b will be given by
View Solution

