Two sides of a rhombus ABCD are parallel to the lines y=x+2 and y=7x+3 If the diagonals of the rhombus intersect at the point (1,2) and the vertex A is on the y-axis, then vertex A can be
If α,β,γ are Acute angles and cosθ=sinβ/sinα,cosφ=sinγsinα andcos(θφ)=sinβsinγ, then the value of tan2α−tan2β−tan2γ is equal to
(0,3)
(0,52)
(0,0)
(0,6)
The correct Answer is:B
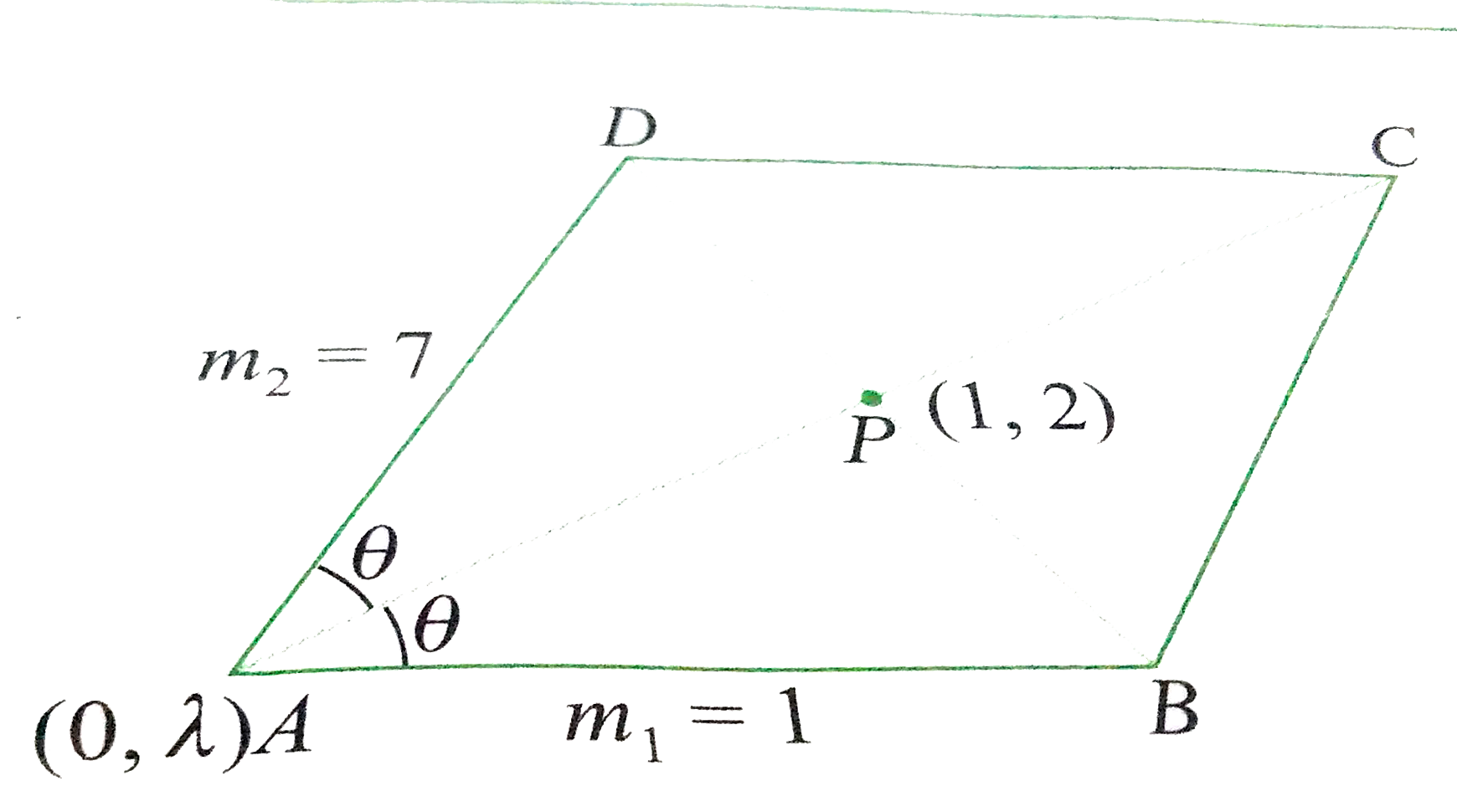
Let point A be (0,λ)
Slope of AP=λ−20−1=2−λ
AB and AC are parallel to the lines y=x+2 and y=7x+3respectively.
Thus, slope of AB and AC are 1 and 7, respectively.
From the figure,
tanθ=(2−λ)−11+(2−λ)=7−(2−λ)1+7(2−λ)
⇒(1−λ3−λ)=(5+λ15−7λ)
⇒(λ−1)(7λ−15)=(5+λ)(3−λ)
⇒8λ20λ=0
A=(0,0)and(0,5/2) .
Topper's Solved these Questions
- COORDINATE SYSYEM Book:CENGAGEChapter:COORDINATE SYSYEM Exercise:Exercise (Comprehension)
Explore 10 Videos
- COORDINATE SYSYEM Book:CENGAGEChapter:COORDINATE SYSYEM Exercise:Exercise (Matrix)
Explore 4 Videos
- COORDINATE SYSYEM Book:CENGAGEChapter:COORDINATE SYSYEM Exercise:Exercise (Single)
Explore 59 Videos
- COORDINATE SYSTEMBook:CENGAGEChapter:COORDINATE SYSTEMExercise:Multiple Correct Answers Type
Explore 2 Videos
- CROSS PRODUCTS Book:CENGAGEChapter:CROSS PRODUCTS Exercise:DPP 2.2
Explore 13 Videos
Similar Questions
Two sides of a rhombus ABCD are parallel to the lines y = x + 2 and y = 7x + 3. If the diagonals of the rhombus intersect at the point (1, 2) and the vertex A is on the y-axis, find the possible coordinates of A. x – y – 1 = 0 are the equations of two internal bisectors of its angles.
View SolutionTwo sides of a Rhombus ABCD are parallel to the lines x−y=5 and 7x−y=3. The diagonals intersect at (2,1) then the equations of the diagonals are
View Solution
Knowledge Check
If α,β,γ are acute angles and cosθ=sinβ/sinα,cosϕ=sinγ/sinα and cos(θ−ϕ)=sinβsinγ, then tan2α−tan2β−tan2γ is equal to
A-1B0C1DNone of theseThe sides of a rhombus ABCD are parallel to the lines x−y+2=0 and 7x−y+3=0, If the diagonals of the rhombus intersect at P(1,2) and the vertex A (different from the origin) is on the y-axis then the ordinate of A is:
A2B52C74D72If α+β=π2and beta+gamma=alpha, thenthevalueoftanalpha is
Atanβ+tanγB2(tanβ+tanγ)Ctanβ+2tanγD2tanβ+tanγ
A rhombus has two of its sides parallel to the lines y=2x+3andy=7x+2. If the diagonals cut at (1, 2) and one vertex is on the y-axis, find the possible values of the ordinate of that vertex.
View SolutionThe sides of a rhombus are parallel to y=2x+3and2y=x+5 . The diagonals of the rhombus intersect at (1, 2). If one vertex of the rhombus lies on the y-axis then possible values of the ordinates of this vertex are 1 (b) 2 (c) 3 (d) 4
View SolutionTwo sides of a rhombus are along the lines,x−y+1=0 and 7x−y−5=0 . If its diagonals intersect at (−1,−2) , then which one of the following is a vertex of this rhombus ?
View SolutionIf tanα,tanβ,tanγ are the roots of the equation x3−px2−r=0, then the value of (1+tan2α)(1+tan2β)(1+tan2γ) is equal to
View SolutionIf 2sinαcosβsinγ=sinβsin(α+γ),thentanα,tanβandγ are in
View Solution