Two tangents PA and PB are drawn to a circle with centre O from an external point P. Prove that $∠ A P B = 2 ∠ O A B$

Video Solution

Text Solution

Verified by Experts

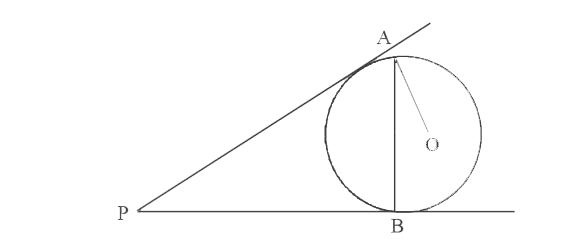
GIVEN A circle with centre $O$ and $P A$ , $P B$ are the tangents on it from a point $P$ outside it.
TO PROVE $∠ A P B = 2 ∠ O A B$ .
PROOF Let $∠ A P B = x^{\circ}$
We know that the tangents to a circle from an external point are equal. So, $P A = P B$
Since the angles opposite to the equal sides of a triangle are equal, so
$P A = P B \Rightarrow ∠ P B A = ∠ P A B$ .
Also, the sum of the angles of a triangle is $180^{\circ}$ .
$∴ ∠ A P B + ∠ P A B + ∠ P B A = 180^{\circ}$
$\Rightarrow x^{\circ} + 2 ∠ P A B = 180^{\circ}$ [ $∵ ∠ P B A = ∠ P A B$ ]
$\Rightarrow ∠ P A B = \frac{1}{2} (180^{\circ} - x^{\circ}) = (90^{\circ} - \frac{1}{2} x^{\circ})$ .
But , $P A$ is a tangent and $O A$ is the radius of the given circle.
$∴ ∠ O A B + ∠ P A B = 90^{\circ}$
$\Rightarrow ∠ O A B = 90^{\circ} - (90^{\circ} - \frac{1}{2} x^{\circ}) \Rightarrow ∠ O A B = \frac{1}{2} x^{\circ} = \frac{1}{2} ∠ A P B$
$\Rightarrow ∠ A P B = 2 ∠ O A B$ .

Updated on:21/07/2023

Two tangents PA and PB are drawn to a circle with centre O from an external point P. If $∠ O A B = 30^{\circ}$ , then $∠ A P B$ is:
केंद्र O वाले वृत्त पर एक बाहरी बिंदु P से दो स्पर्श रेखाएँ PA तथा PB खींची जाती हैं | यदि $∠ O A B = 30^{\circ}$ है, तो $∠ A P B$ का मान क्या होगा ?
A $15^{\circ}$
B $30^{\circ}$
C $120^{\circ}$
D $60^{\circ}$
From a point P two tangents PA and PB are drawn to a circle with centre O.if OP is equal to diameter of the circle then $∠ A P B$ is
A $60^{\circ}$
B $45^{\circ}$
C $90^{\circ}$
D $30^{\circ}$
From a point P, two tangents PA and PB are drawn to a circle with centre O. If OP is equal to diameter of the circle, then $∠ A P B$ is
A $45^{\circ}$
B $90^{\circ}$
C $30^{\circ}$
D $60^{\circ}$