Question

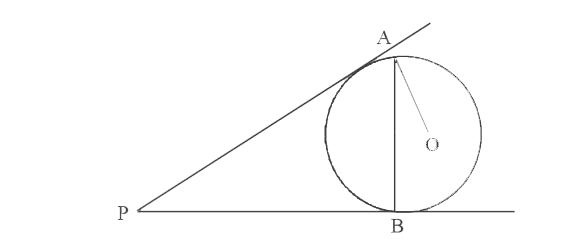
Two tangents PA and PB are drawn to a circle with centre O from an external point P. If $\angle OAB={30}^{\circ }$, then $\angle APB$ is:
केंद्र O वाले वृत्त पर एक बाहरी बिंदु
P से दो स्पर्श रेखाएँ PA तथा PB खींची जाती हैं | यदि $\angle OAB={30}^{\circ }$ है, तो $\angle APB$ का मान क्या होगा ?

Options

A. `120^@`
B. `60^@`
C. `30^@`
D. `15^@`

Explanation

To find the angle $$APB$$ given that $$\angle OAB={30}^{\circ }$$, we can follow these steps:

1. Understand the Configuration:
- We have a circle with center \( O \) and an external point \( P \) from which two tangents \( PA \) and \( PB \) are drawn to the circle at points \( A \) and \( B \) respectively.

2. Identify Known Angles:
- We know that \( \angle OAB = 30^\circ \). Since \( OA \) is the radius of the circle and \( PA \) is a tangent, \( OA \) is perpendicular to \( PA \). Therefore, \( \angle OAP = 90^\circ \).

3. Use Triangle Properties:
- In triangle \( OAP \), we can find \( \angle OAP \) using the fact that the sum of angles in a triangle is \( 180^\circ \):
\( \angle OAP + \angle OAB + \angle APB = 180^\circ \)
- Substituting the known values:
\( 90^\circ + 30^\circ + \angle APB = 180^\circ \)

4. Solve for \( \angle APB \):
- Rearranging the equation gives:
\( \angle APB = 180^\circ - 90^\circ - 30^\circ \)
\( \angle APB = 60^\circ \)

5. Conclusion:
- Therefore, the measure of \( \angle APB \) is \( 60^\circ \).

Final Answer:
\( \angle APB = 60^\circ \)