Two variable chords ABandBC of a circle x2+y2=r2 are such that AB=BC=r . Find the locus of the point of intersection of tangents at AandC.
The correct Answer is:x2+y2=4r2
Let the point of intersection of tangents at A and be P≡(x,y) .
Since AB=AO=BO=r, we get
∠AOB=60∘
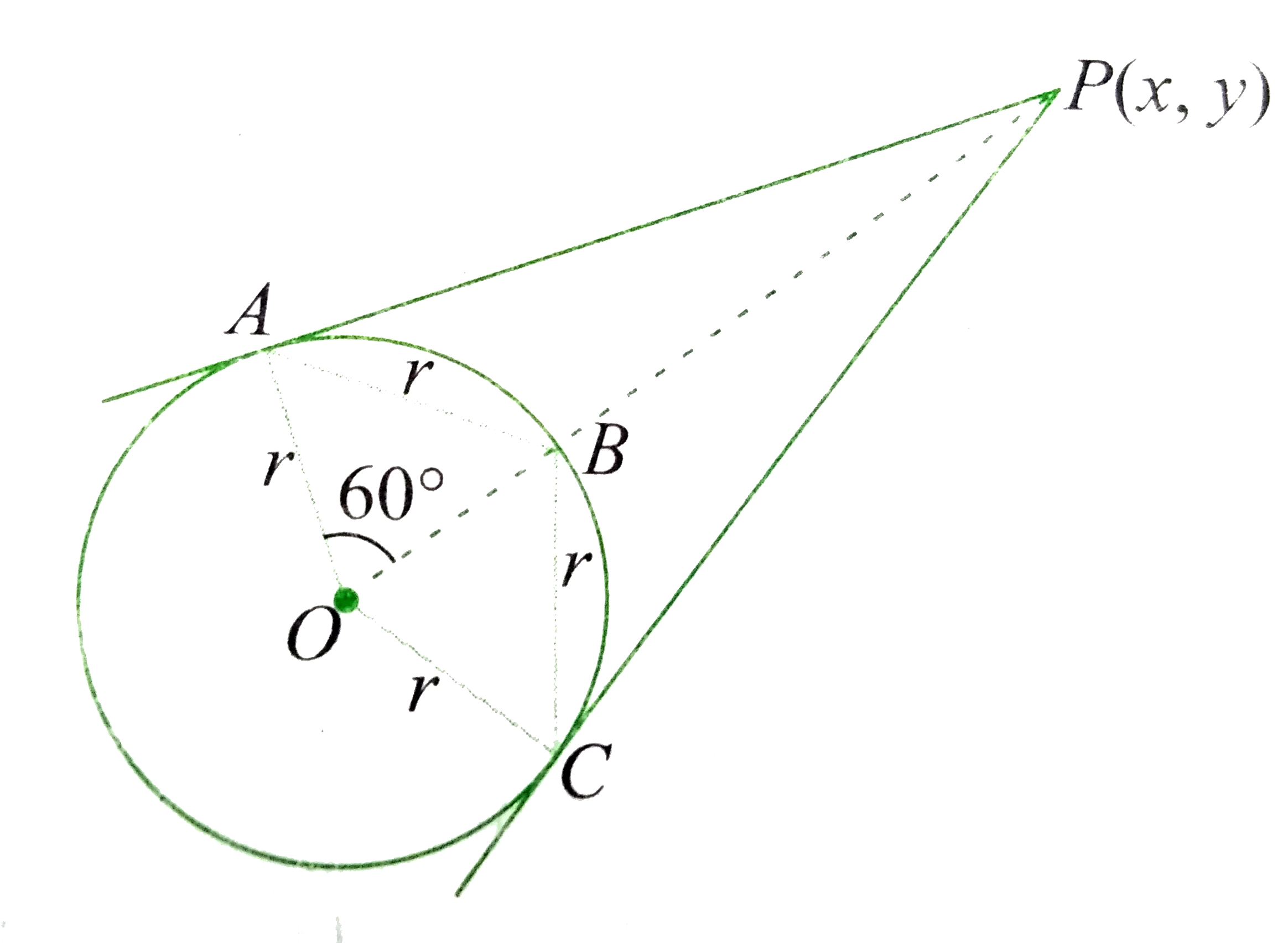
or PArtan60∘=√3
or √x2+y2−r2=√3r
Therefore, x2+y2=4r2 is the locus of the point P.
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.16
3 Videos
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.17
2 Videos
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.14
4 Videos
- BINOMIAL THEOREMBOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix
4 Videos
- CIRCLESBOOK - CENGAGE ENGLISHCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
Two variable chords AB and BC of a circle x2+y2=a2 are such that AB=BC=a. M and N are the midpoints of AB and BC, respectively, such that the line joining MN intersects the circles at P and Q, where P is closer to AB and O is the center of the circle.
The locus of the points of intersection of tangents at A and C is
View SolutionTwo variable chords AB and BC of a circle x2+y2=a2 are such that AB=BC=a. M and N are the midpoints of AB and BC, respectively, such that the line joining MN intersects the circles at P and Q, where P is closer to AB and O is the center of the circle.
The locus of the points of intersection of tangents at A and C is
View SolutionA chord AB of circle x2+y2=a2 touches the circle x2+y2−2ax=0.Locus of the point of intersection of tangens at A and B is :
View SolutionIf the tangents to the parabola y2=4ax intersect the hyperbola x2a2−y2b2=1 at AandB , then find the locus of the point of intersection of the tangents at AandB.
View SolutionIf there are two points AandB on rectangular hyperbola xy=c2 such that abscissa of A= ordinate of B, then locusof point of intersection of tangents at AandB is (a) y2−x2=2c2 (b) y2−x2=c22 (c) y=x (d) non of these
View SolutionIf a tangent to the parabola y2=4ax intersects the x2a2+y2b2=1 at Aand B, then the locus of the point of intersection of tangents at A and B to the ellipse is
View SolutionFind the locus of the point of intersection of perpendicular tangents to the circle x2+y2=4
View SolutionThe tangents PA and PB are drawn from any point P of the circle x2+y2=2a2 to the circle x2+y2=a2. The chord of contact AB on extending meets again the first circle at the points A' and B'. The locus of the point of intersection of tangents at A' and B' may be given as
View SolutionA variable chord of circle x2+y2+2gx+2fy+c=0 passes through the point P(x1,y1). Find the locus of the midpoint of the chord.
View SolutionThe equation of the locus of the middle point of a chord of the circle x2+y2=2(x+y) such that the pair of lines joining the origin to the point of intersection of the chord and the circle are equally inclined to the x-axis is x+y=2 (b) x−y=2 2x−y=1 (d) none of these
View Solution
