Question

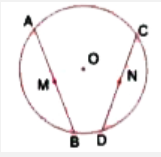
Two variable chords AB and BC of a circle $x^2+y^2=a^2$ are such that $AB=BC=a$. M and N are the midpoints of AB and BC, respectively, such that the line joining MN intersects the circles at P and Q, where P is closer to AB and O is the center of the circle.
The locus of the points of intersection of tangents at A and C is

Options

A. (a)`60^(@)`
B. (b)`90^(@)`
C. (c)`120^(@)`
D. (d)`150^(@)`

Answer

A

Explanation

To solve the problem step by step, we will analyze the given information and derive the required locus of the points of intersection of the tangents at points A and C.

Step 1: Understand the Circle and Chords
The equation of the circle is given by \( x^2 + y^2 = a^2 \). The points A, B, and C are on the circle such that the lengths of chords AB and BC are equal to \( a \).

Hint: Visualize the circle and mark points A, B, and C such that the lengths of the chords are equal.

Step 2: Determine the Midpoints
Let M and N be the midpoints of chords AB and BC, respectively. The coordinates of M and N can be expressed in terms of the coordinates of points A and B, and B and C.

Hint: Use the midpoint formula: if \( M \) is the midpoint of \( AB \), then \( M = \left( \frac{x_A + x_B}{2}, \frac{y_A + y_B}{2} \right) \).

Step 3: Analyze the Line Joining M and N
The line segment joining M and N will intersect the circle at points P and Q. Since P is closer to AB, we need to find the coordinates of P and Q based on the geometry of the circle.

Hint: Use the properties of the circle and the midpoints to derive the equations of the line MN.

Step 4: Tangents at Points A and C
The tangents at points A and C can be derived using the point of tangency and the radius. The angle between these tangents can be determined using the geometry of the circle.

Hint: Recall that the angle between two tangents drawn from an external point to a circle can be calculated using the angle subtended by the points at the center.

Step 5: Calculate the Angle Between Tangents
Since triangle AOB is equilateral (as \( AB = BC = a \)), we know that each angle in triangle AOB is \( 60^\circ \). The angle \( AOC \) can be found as follows:
- The angle \( AOB \) is \( 60^\circ \).
- The angle \( BOC \) is also \( 60^\circ \).
- Therefore, the angle \( AOC = 120^\circ \).

Hint: Use the property of angles in a triangle and the fact that the sum of angles on a straight line is \( 180^\circ \).

Step 6: Conclusion
The angle between the tangents at points A and C is \( 60^\circ \). Thus, the locus of the points of intersection of the tangents at A and C is determined.

Final Answer: The angle between the tangents at points A and C is \( 60^\circ \).