Using ruler and compasses only, construct a from the following data:
To construct triangle ABC given that AB+BC+CA=12 cm, ∠B=45∘, and ∠C=60∘, follow these steps:
Step-by-Step Construction:
1. Draw a Line Segment:
- Draw a line segment PQ of length 12 cm. This will represent the perimeter of triangle ABC.
- Hint: Use a ruler to measure exactly 12 cm.
2. Label the Points:
- Label point P as point A and point Q as point B.
- Hint: Ensure that the labels are clear to avoid confusion later.
3. Construct Angle B (45°):
- At point A, use a compass to draw a semicircle with a radius that can reach point Q.
- Mark the intersection points of the semicircle with the line segment.
- Using the compass, draw arcs from these intersection points to create two points that will help form a 90° angle. Bisect this angle to get a 45° angle at point A.
- Hint: The intersection of the arcs will help you find the angle bisector accurately.
4. Construct Angle C (60°):
- At point B, repeat the process to construct a 60° angle. Draw a semicircle centered at B and mark the intersection points.
- Use the compass to create arcs from these points to find the intersection that gives you a 60° angle at point B.
- Hint: Remember that a 60° angle can be constructed using the same radius for all arcs.
5. Locate Point C:
- Extend the lines from points A and B until they intersect. Label this intersection point as C.
- Hint: Ensure that the lines are extended far enough for them to intersect.
6. Complete the Triangle:
- Connect points A, B, and C to complete triangle ABC.
- Hint: Use a ruler to draw straight lines between the points.
7. Verify the Construction:
- Check that the angles ∠A, ∠B, and ∠C add up to 180° and that the perimeter is 12 cm.
- Hint: Measure the sides to confirm the perimeter and use a protractor to check the angles if necessary.
Final Diagram:
- You should now have triangle ABC with the specified angles and perimeter.
- Draw a line segment PQ of length 12 cm. This will represent the perimeter of triangle ABC.
- Hint: Use a ruler to measure exactly 12 cm.
- Label point P as point A and point Q as point B.
- Hint: Ensure that the labels are clear to avoid confusion later.
- At point A, use a compass to draw a semicircle with a radius that can reach point Q.
- Mark the intersection points of the semicircle with the line segment.
- Using the compass, draw arcs from these intersection points to create two points that will help form a 90° angle. Bisect this angle to get a 45° angle at point A.
- Hint: The intersection of the arcs will help you find the angle bisector accurately.
- At point B, repeat the process to construct a 60° angle. Draw a semicircle centered at B and mark the intersection points.
- Use the compass to create arcs from these points to find the intersection that gives you a 60° angle at point B.
- Hint: Remember that a 60° angle can be constructed using the same radius for all arcs.
- Extend the lines from points A and B until they intersect. Label this intersection point as C.
- Hint: Ensure that the lines are extended far enough for them to intersect.
- Connect points A, B, and C to complete triangle ABC.
- Hint: Use a ruler to draw straight lines between the points.
- Check that the angles ∠A, ∠B, and ∠C add up to 180° and that the perimeter is 12 cm.
- Hint: Measure the sides to confirm the perimeter and use a protractor to check the angles if necessary.
- You should now have triangle ABC with the specified angles and perimeter.
Topper's Solved these Questions
Similar Questions
In a ABC, D and E are points on the sides AB and AC respectively. For each of the following cases show that DEBC : AB=12 cm, AD=8 cm, AE=12 cm and AC=18 cm . (ii) AB=5.6 cm, AD=1.4 cm, AC=7.2 cm and AE=1.8 cm
View SolutionIn Fig. 4.60, check whether AD is the bisector of ∠A of ABC in each of the following: (FIGURE) AB=5cm, AC=10cm, BD=1.5cm and CD=3.5cm (ii) AB=4cm, AC=6cm, BD=1.6cm and CD=2.4cm (iii) AB=8cm, AC=24cm, BD=6cm and BC=24cm
View SolutionIf ABC and DEF are two triangles such that ABC ≅FDE and AB=5cm, ∠B=400 and ∠A=800. Then, which of the following is true? DF=5cm, ∠F=600 (b) DE=5cm, ∠E=600 DF=5 cm, ∠E=600 (d) DE=5cm, ∠D=400
View SolutionIn Fig. 4.60, check whether AD is the bisector of ∠A of ABC in each of the following: (FIGURE) AB=6cm, AC=8cm, BD=1.5cm and CD=2cm (ii) AB=5cm, AC=12cm , BD=2.5cm and BC=9cm
View SolutionIn which of the following cases can a right triangle ABC be constructed? AB=5 cm, BC=7 cm, AC=10 cm AB=7 cm, BC=8 cm, AC=12 cm AB=8 cm, BC=17 cm, AC=15 cm None of these
View SolutionIn a parallelogram ABCD, the diagonals bisect each other at O. If ∠ABC=300, ∠BDC=100and ∠CAB=700, Find: ∠DAB, ∠ADC, ∠BCD, ∠AOD, ∠DOC, ∠BOC, ∠AOB, ∠ACD, ∠CAB, ∠ADB
Given that
∠ABC=302,∠ABC=∠ADC=300
[We know that measure of opposite angles are equal in a parallelogram]
∠BDC=100
∠CAB=700
∠BDA=∠ADB=∠ADC–∠BDC
302–102=202
∠DAB=1800–300=1500
∠ADB=∠DBC=200 (alternate angles)
∠BCD=∠DAB=1500
[we know, opposite angles are equal in a parallelogram]
∠DBA=∠BDC=100
[we know, Alternate interior angles are equal]
InΔABC
∠CAB+∠ABC+∠BCA=1800
[since, sum of all angles of a triangle is 180^0]
700+300+∠BCA=1800
∠BCA=1800–1000=800
∠DAB=∠DAC+∠CAB=700+800=1500
∠BCD=1500 (opposite angle of the parallelogram)
∠DCA=∠CAB=700
In ΔDOC∠BDC+∠ACD+∠DOC=1800
[since, sum of all angles of a triangle is 180^0]
100+700+∠DOC=1800
∠DOC=1800−800
∠ACB=800
View SolutionIn a rhombus ABCD, if ∠ACB=40∘, then ∠ADB=(a) 70∘ (b) 45∘ (c) 50∘ (d) 60∘
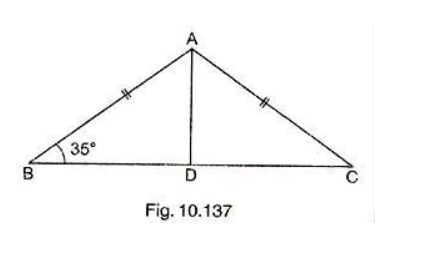
View SolutionABC is an isosceles triangle such that AB=ACandAD is the median to base BC . Then, ∠BAD=
(a) 55∘
(b) 70∘
(c) 35∘
(d) 110∘
View SolutionLine segments AB and CD intersect at O such that AC∣∣DB. If ∠CAB=450and ∠CDB=550, then ∠BOD= 1000 (b) 800 (c) 900 (d) 1350
View SolutionDraw a triangle ABC with AB=6 cm, BC=7 cm and CA=8 cm. Using ruler and compass alone, draw (i) the bisector AD of ∠A and (ii) perpendicular AL from A on BC. Measure LAD.
View Solution
