Which of the following pairs of triangle are congruent by ASA condition?
To determine which pairs of triangles are congruent by the ASA (Angle-Side-Angle) condition, we will analyze the given triangles step by step.
1. Identify the Triangles:
We have two triangles, triangle AOB and triangle DOC.
2. Check the Given Measurements:
- We know that the length of side AB is equal to the length of side CD. Specifically, AB = CD = 6.1 cm.
- We also know that angle B is equal to angle D. Specifically, angle B = angle D = 45 degrees.
3. Identify Vertically Opposite Angles:
- Angle AOB and angle COD are vertically opposite angles. By the property of vertically opposite angles, we know that angle AOB = angle COD.
4. Summarize the Known Values:
- We have:
- AB = CD (6.1 cm)
- Angle B = Angle D (45 degrees)
- Angle AOB = Angle COD (vertically opposite angles)
5. Apply the ASA Condition:
- The ASA condition states that if two angles and the included side of one triangle are equal to two angles and the included side of another triangle, then the triangles are congruent.
- In our case:
- We have two angles (angle B and angle D) that are equal.
- We have the side AB equal to side CD.
- We have the angle AOB equal to angle COD.
- Thus, we can conclude that triangle AOB is congruent to triangle DOC by the ASA condition.
Conclusion:
Therefore, triangle AOB is congruent to triangle DOC by the ASA condition.
We have two triangles, triangle AOB and triangle DOC.
- We know that the length of side AB is equal to the length of side CD. Specifically, AB = CD = 6.1 cm.
- We also know that angle B is equal to angle D. Specifically, angle B = angle D = 45 degrees.
- Angle AOB and angle COD are vertically opposite angles. By the property of vertically opposite angles, we know that angle AOB = angle COD.
- We have:
- AB = CD (6.1 cm)
- Angle B = Angle D (45 degrees)
- Angle AOB = Angle COD (vertically opposite angles)
- The ASA condition states that if two angles and the included side of one triangle are equal to two angles and the included side of another triangle, then the triangles are congruent.
- In our case:
- We have two angles (angle B and angle D) that are equal.
- We have the side AB equal to side CD.
- We have the angle AOB equal to angle COD.
- Thus, we can conclude that triangle AOB is congruent to triangle DOC by the ASA condition.
Therefore, triangle AOB is congruent to triangle DOC by the ASA condition.
Topper's Solved these Questions
Similar Questions
Which of the following pairs of triangles are congruent ? Also state the condition of congruency in each case :

(iv) In ΔABC and ΔDEF,AB=EF,BC=DF and ∠B=∠F
(v) In ΔABC and ΔPQR,AB=QR,AC=PR and ∠B=∠R
(vi) In ΔABC and ΔPQR,∠A=∠P,AC=PR and AB=PQ
(vi) In ΔABC and ΔPQR,AB=QR,∠A=∠Q and AC=QP.
View SolutionWhich of the following pairs of triangles are congruent ? In each case, state the condition of congruency :
(a) In ΔABCandΔDEF, AB = DE, BC = EF and ∠B=∠E.
(b) In ΔABCandΔDEF,∠B=∠E=90∘, AC = DF and BC = EF.
(c) In ΔABCandΔQRP, AB = QR, ∠B=∠Rand∠C=∠P.
(d) In ΔABCandΔPQR, AB = PQ, AC = PR and BC = QR.
(e) In ΔABCandΔPQR, BC = QR, ∠A=90∘,∠C=∠R=40∘and∠Q=50∘.
View Solution
Knowledge Check
Which of the following is the conditional p→q is
Aq is sufficient for pBp is necessary for qCif p then qDIf q then pWhich of the following pair represent pair of diastereomers ?
AMeso tartaric acid and (l) tartaric acidB C
C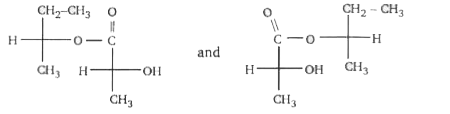 DAll of these
DAll of these
State giving reasons, whether the following pairs of triangles are congruent or not: ΔKLM in which KM=4 cm ∠K=75∘,∠M=40∘ and ΔPQR in which PR=4 cm, ∠Q=65∘,∠R=40∘.
View SolutionState giving reasons, whether the following pairs of triangles are congruent or not: ΔDEF in which ∠E=48∘,DE=6cm,EF=8cm and ΔMNR in which ∠R=48∘,MN=6cm,MR=8cm
View SolutionState giving reasons, whether the following pairs of triangles are congruent or not: ΔABC in which AB=3 cm ∠A=90∘, BC=5 cm and ΔKLM in which KM=3 cm ∠K=90∘ cm, 1,M=5cm
View SolutionState giving reasons, whether the following pairs of triangles are congruent or not: ΔABC in which ∠A=50∘,∠B=60∘,BC=4.5 cm and ΔDEFo in which ∠E=60∘,EF=4.5cm,∠F=70∘
View SolutionIn each of the following pairs of triangles the measure of some parts are indicated along. Side. By the application of SAS congruence condition, state which are congruent. State the result in symbolic form.
View SolutionIn the following pairs of triangle (Fig.10), by applying SSS condition, state which are congruent. State the result in symbolic form:
View Solution
