Write true or false and state reason:
If angle between two tangents drawn from a point P to a circle of radius a and centre O is 90∘ then OP=a√2.
true
false
can not determine
none of these
The correct Answer is:A
To determine whether the statement "If the angle between two tangents drawn from a point P to a circle of radius a and center O is 90 degrees, then OP = a√2" is true or false, we can follow these steps:
1. Understanding the Setup:
- We have a circle with center O and radius a.
- From point P, two tangents PT and PR are drawn to the circle, creating an angle ∠TPR of 90 degrees.
2. Identifying Key Angles:
- Since PT and PR are tangents to the circle, they are perpendicular to the radius at the point of tangency. Therefore, ∠OTP = 90 degrees, where T is the point of tangency.
3. Using the Properties of Angles:
- The angle ∠TPR is given as 90 degrees. By the property of tangents, we know that the angle bisector OP divides this angle into two equal angles. Thus, ∠TPO = ∠RPO = 45 degrees.
4. Analyzing Triangle PTO:
- Triangle PTO is a right-angled triangle with:
- ∠TPO = 45 degrees
- OT (the radius) = a
- OP (the distance from point P to center O) is the hypotenuse.
5. Applying Trigonometric Ratios:
- In triangle PTO, we can use the sine function:
sin(45∘)=OppositeHypotenuse=TOOP
- We know that sin(45∘)=1√2 and TO = a (the radius).
6. Setting Up the Equation:
- Plugging in the known values:
1√2=aOP
- Rearranging gives:
OP=a⋅√2
7. Conclusion:
- The derived result shows that OP = a√2, which matches the statement given in the question.
Final Answer:
- The statement is True.
- We have a circle with center O and radius a.
- From point P, two tangents PT and PR are drawn to the circle, creating an angle ∠TPR of 90 degrees.
- Since PT and PR are tangents to the circle, they are perpendicular to the radius at the point of tangency. Therefore, ∠OTP = 90 degrees, where T is the point of tangency.
- The angle ∠TPR is given as 90 degrees. By the property of tangents, we know that the angle bisector OP divides this angle into two equal angles. Thus, ∠TPO = ∠RPO = 45 degrees.
- Triangle PTO is a right-angled triangle with:
- ∠TPO = 45 degrees
- OT (the radius) = a
- OP (the distance from point P to center O) is the hypotenuse.
- In triangle PTO, we can use the sine function:
sin(45∘)=OppositeHypotenuse=TOOP
- We know that sin(45∘)=1√2 and TO = a (the radius).
- Plugging in the known values:
1√2=aOP
- Rearranging gives:
OP=a⋅√2
- The derived result shows that OP = a√2, which matches the statement given in the question.
- The statement is True.
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - EXERCISE 9.3 SHORT ANSWER TYPE QUESTIONS10videos
CIRCLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - EXERCISE 9.4 LONG ANSWER TYPE QUESTIONS14videos
CIRCLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - EXERCISE 9.4 LONG ANSWER TYPE QUESTIONS14videos
CIRCLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - Long Answer Type Questions10videos
ARITHMETIC PROGRESSIONS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - Exercise 10.4 Long Answer type Questions7videos
CONSTRUCTIONS
Similar Questions
Write True or False and justify your answer:
If angle between two tangents drawn from a point P to a circle of radius a and centre O is 60∘ then OP=a√3.View SolutionIf the angle between two tangents drawn from an external point P to a circle of radius 'a' and centre O, is 60∘, then find the length of OP.
View SolutionIf the angle between two tangents drawn from an external point ‘P’ to a circle of radius ‘r’ and centre O is 60∘, then find the length of OP.
View SolutionFind the angle between two tangents drawn from the point ( 1,4) to the parabola y2=12x
View SolutionShow that the angle between the tangents drawn from (-1,3) to the circle x2+y2=5 is 90∘.
View SolutionThe length of tangent from an external point P on a circle with centre 0 is always less than OP.
View SolutionIn figure, From an external point P, Two tangents PQ and PR are drawn to a circle of radius 4 cm with centre O . If ∠QPR=90∘ then length of PQ is
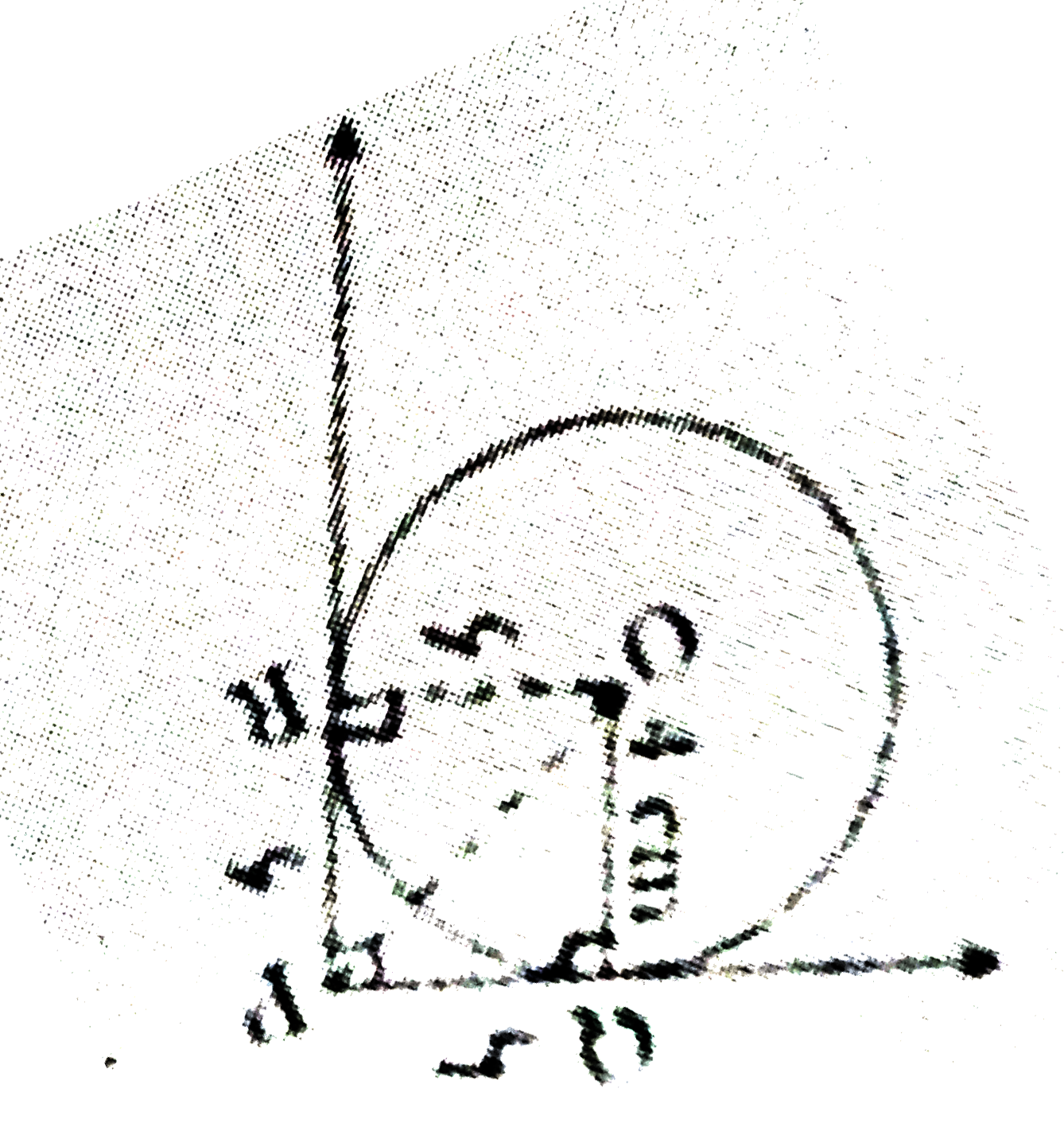 View Solution
View SolutionIf Figure-1, from an external point P, two tangents PQ and PR are drawn to a circle of radius 4 cm with centre O. if ∠QPR=90∘, then length of PQ is
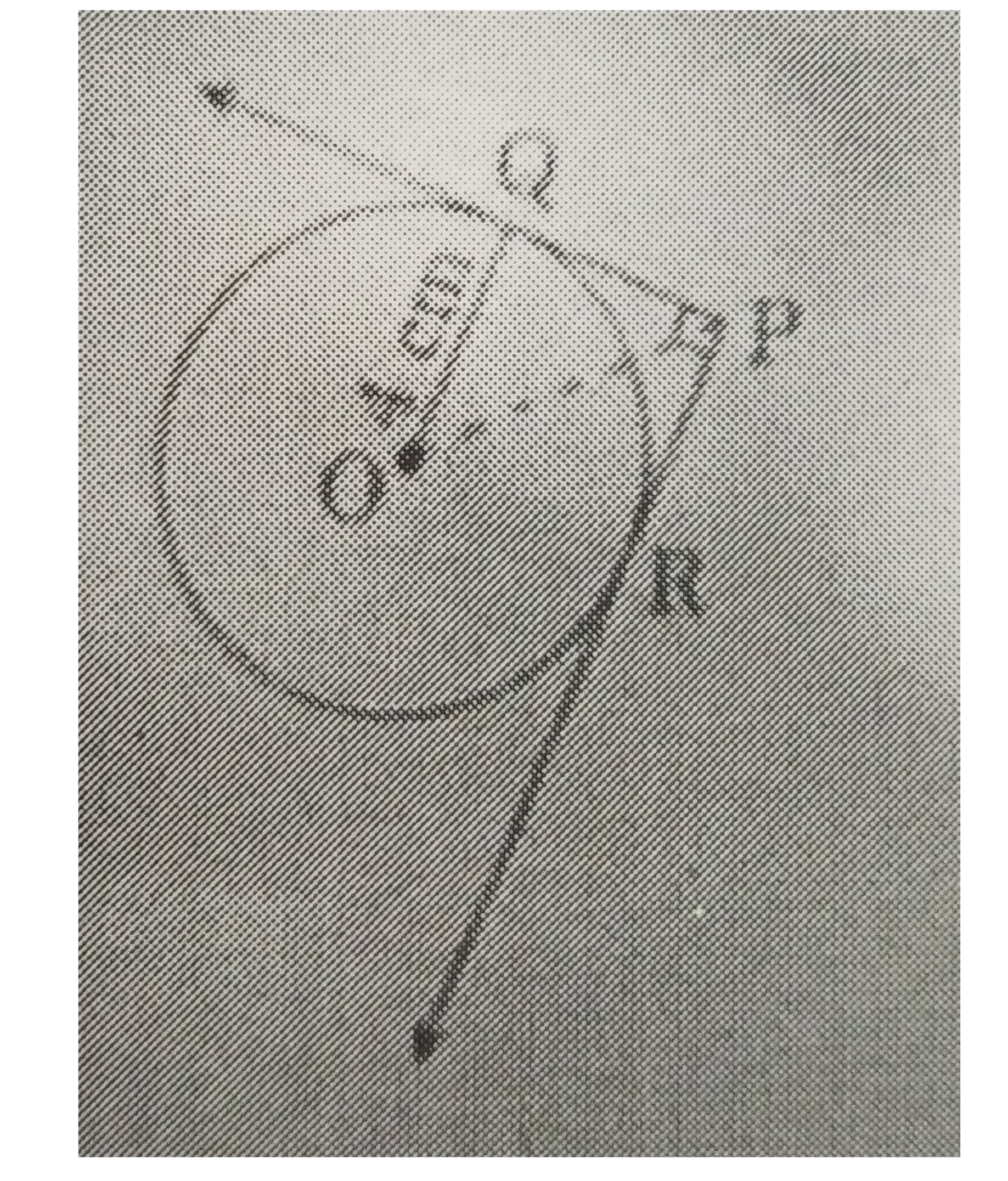 View Solution
View SolutionThe angle between the tangents drawn from a point on the director circle x2+y2=50 to the circle x2+y2=25, is
View SolutionThe angle between a pair of tangents drawn from a point P to the hyperbola y2=4ax is 45∘. Show that the locus of the point P is hyperbola.
View Solution

