x+2y≤10,x+y≥1,x−y≤0,x≥0,y≥0
Text Solution
The correct Answer is:N/a
First inequation : x+2y≤10
Corresponding equation : x+2y=10
This line passes through the points A(10, 0) and B(0, 5). Join AB.
At point (0, 0) , from the inequation, 0le10 (True)
∴The Solution of this inequation is that region of XY-plane divided by line AB in which (0, 0) lie.
Second inequation : x+y≥1
Corresponding equation: x+y=1
This line passes through the points C(1, 0) and D(0, 1). join CD.
At point (0, 0), From the inequation, 0≥1 (False)
∴ The solution of this inequation is that region of XY-plane divided by line AB in which (0, 0) lie.
Third inequation : x−y≤0
Corresponding inequation : x−y=0
This line passes through the points O(0, 0) and E(2, 2) . Join OE.
At point (1, 0 ), from the inequation, 1≥0 (False)
:, The solution of this inequation is that region of XY-plane divided by line OE in which (1, 0) does not lie.
The solution of x≥ 0, y ≥ 0 is in first quadrant
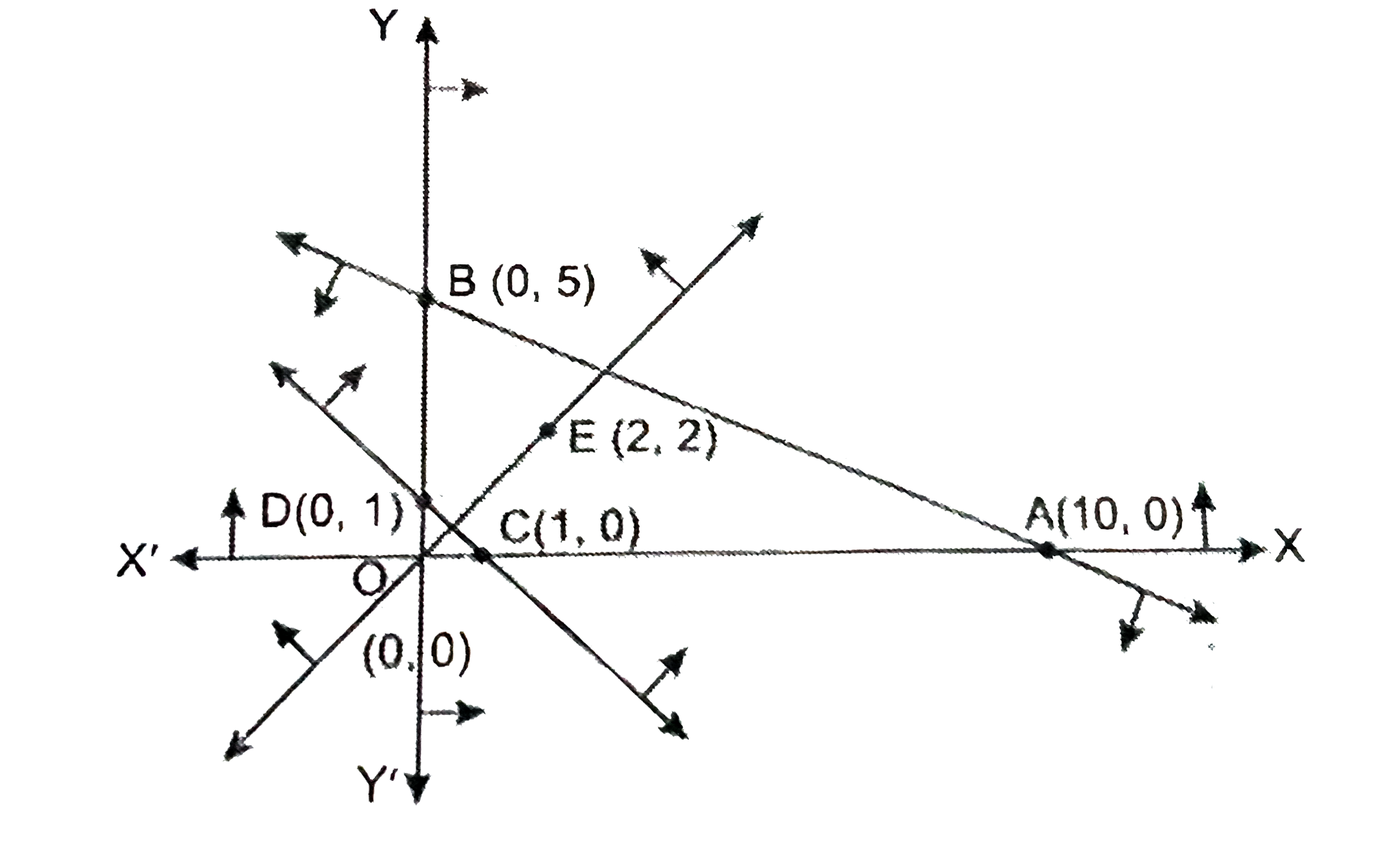
∴ The solution of given inequation is shown by the shaded region.
|
Topper's Solved these Questions
- LINEAR INEQUALITIESBOOK - NAGEEN PRAKASHANCHAPTER - LINEAR INEQUALITIESEXERCISE - MISCELLANEOUS EXERCISE
14 Videos
- LINEAR INEQUALITIESBOOK - NAGEEN PRAKASHANCHAPTER - LINEAR INEQUALITIESEXERCISE - EXERCISE
76 Videos
- LIMITS AND DERIVATIVESBOOK - NAGEEN PRAKASHANCHAPTER - LIMITS AND DERIVATIVESEXERCISE - Miscellaneous Exercise
30 Videos
- MATHEMATICAL REASONING BOOK - NAGEEN PRAKASHANCHAPTER - MATHEMATICAL REASONING EXERCISE - Misellaneous exercise
7 Videos
Similar Questions
x+2y≤10,x+y≥1,x−y≤0,x≥0,y≥0
View Solutionx+2y≤10,x+y≥1,x−y≤0,x≥0,y≥0
View SolutionZ=5x+10y
x+2y≤120,x+y≥60,x−2y≥0,x≥0,y≥0.
View Solutiony−2x≤1,x+y≤2,x≥0,y≥0
View Solutiony−2x≤1,x+y≤2,x≥0,y≥0
View Solution2x+y≤6,x+2y≤8,x≥0,y≥0
View Solution2x+y≤6,x+2y≤8,x≥0,y≥0
View SolutionZ=3x+9y
x+3y≤60,x+y≥10,x≤y,x≥0,y≥0
View Solution2x+y≥2,x−y≤1,x+2y≤8,x≥0,y≥0.
View Solutionx+2y≤40,2x+y≤40,x≥0,y≥0
View Solution
